eqtools package

Submodules

eqtools.AUGData module

This module provides classes inheriting eqtools.Equilibrium for working with ASDEX Upgrade experimental data.

class eqtools.AUGData.AUGDDData(shot, shotfile='EQH', edition=0, shotfile2=None, length_unit='m', tspline=False, monotonic=True, experiment='AUGD')[source]

Bases: eqtools.core.Equilibrium

Inherits eqtools.Equilibrium class. Machine-specific data handling class for ASDEX Upgrade. Pulls AFS data from selected location and shotfile, stores as object attributes. Each data variable or set of variables is recovered with a corresponding getter method. Essential data for mapping are pulled on initialization (e.g. psirz grid). Additional data are pulled at the first request and stored for subsequent usage.

Intializes ASDEX Upgrade version of the Equilibrium object. Pulls data to storage in instance attributes. Core attributes are populated from the AFS data on initialization. Additional attributes are initialized as None, filled on the first request to the object.

Parameters:

shot (integer) – ASDEX Upgrade shot index.
Keyword Arguments:
 
  • shotfile (string) – Optional input for alternate shotfile, defaults to ‘EQH’ (i.e., CLISTE results are in EQH,EQI with other reconstructions Available (FPP, EQE, ect.).
  • edition (integer) – Describes the edition of the shotfile to be used
  • shotfile2 (string) – Describes companion 0D equilibrium data, will automatically reference based off of shotfile, but can be manually specified for unique reconstructions, etc.
  • length_unit (string) –

    Sets the base unit used for any quantity whose dimensions are length to any power. Valid options are:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ whatever the default in the tree is (no conversion is performed, units may be inconsistent)

    Default is ‘m’ (all units taken and returned in meters).

  • tspline (Boolean) – Sets whether or not interpolation in time is performed using a tricubic spline or nearest-neighbor interpolation. Tricubic spline interpolation requires at least four complete equilibria at different times. It is also assumed that they are functionally correlated, and that parameters do not vary out of their boundaries (derivative = 0 boundary condition). Default is False (use nearest neighbor interpolation).
  • monotonic (Boolean) – Sets whether or not the “monotonic” form of time window finding is used. If True, the timebase must be monotonically increasing. Default is False (use slower, safer method).
  • experiment – Used to describe the work space that the shotfile is located It defaults to ‘AUGD’ but can be set to other values
getInfo()[source]

returns namedtuple of shot information

Returns:namedtuple containing
shot ASDEX Upgrage shot index (long)
tree shotfile (string)
nr size of R-axis for spatial grid
nz size of Z-axis for spatial grid
nt size of timebase for flux grid
getTimeBase()[source]

returns time base vector.

Returns:[nt] array of time points.
Return type:time (array)
Raises:ValueError – if module cannot retrieve data from the AUG AFS system.
getFluxGrid()[source]

returns flux grid.

Note that this method preserves whatever sign convention is used in AFS.

Returns:[nt,nz,nr] array of (non-normalized) flux on grid.
Return type:psiRZ (Array)
Raises:ValueError – if module cannot retrieve data from the AUG AFS system.
getRGrid(length_unit=1)[source]

returns R-axis.

Returns:[nr] array of R-axis of flux grid.
Return type:rGrid (Array)
Raises:ValueError – if module cannot retrieve data from the AUG AFS system.
getZGrid(length_unit=1)[source]

returns Z-axis.

Returns:[nz] array of Z-axis of flux grid.
Return type:zGrid (Array)
Raises:ValueError – if module cannot retrieve data from the AUG AFS system.
getFluxAxis()[source]

returns psi on magnetic axis.

Returns:[nt] array of psi on magnetic axis.
Return type:psiAxis (Array)
Raises:ValueError – if module cannot retrieve data from the AUG AFS system.
getFluxLCFS()[source]

returns psi at separatrix.

Returns:[nt] array of psi at LCFS.
Return type:psiLCFS (Array)
Raises:ValueError – if module cannot retrieve data from the AUG AFS system.
getFluxVol(length_unit=3)[source]

returns volume within flux surface.

Keyword Arguments:
 length_unit (String or 3) – unit for plasma volume. Defaults to 3, indicating default volumetric unit (typically m^3).
Returns:[nt,npsi] array of volume within flux surface.
Return type:fluxVol (Array)
Raises:ValueError – if module cannot retrieve data from the AUG AFS system.
getVolLCFS(length_unit=3)[source]

returns volume within LCFS.

Keyword Arguments:
 length_unit (String or 3) – unit for LCFS volume. Defaults to 3, denoting default volumetric unit (typically m^3).
Returns:[nt] array of volume within LCFS.
Return type:volLCFS (Array)
Raises:ValueError – if module cannot retrieve data from the AUG AFS system.
getRmidPsi(length_unit=1)[source]

returns maximum major radius of each flux surface.

Keyword Arguments:
 length_unit (String or 1) – unit of Rmid. Defaults to 1, indicating the default parameter unit (typically m).
Returns:[nt,npsi] array of maximum (outboard) major radius of flux surface psi.
Return type:Rmid (Array)
Raises:NotImplementedError – Not implemented on ASDEX-Upgrade reconstructions.
getRLCFS(length_unit=1)[source]

returns R-values of LCFS position.

Returns:[nt,n] array of R of LCFS points.
Return type:RLCFS (Array)
Raises:ValueError – if module cannot retrieve data from the AUG AFS system.
getZLCFS(length_unit=1)[source]

returns Z-values of LCFS position.

Returns:[nt,n] array of Z of LCFS points.
Return type:ZLCFS (Array)
Raises:ValueError – if module cannot retrieve data from the AUG AFS system.
remapLCFS(mask=False)[source]

Overwrites RLCFS, ZLCFS values pulled with explicitly-calculated contour of psinorm=1 surface. This is then masked down by the limiter array using core.inPolygon, restricting the contour to the closed plasma surface and the divertor legs.

Keyword Arguments:
 

mask (Boolean) – Default False. Set True to mask LCFS path to limiter outline (using inPolygon). Set False to draw full contour of psi = psiLCFS.
Raises:
  • NotImplementedError – if matplotlib.pyplot is not loaded.
  • ValueError – if limiter outline is not available.
getF()[source]

returns F=RB_{Phi}(Psi), often calculated for grad-shafranov solutions.

Returns:[nt,npsi] array of F=RB_{Phi}(Psi)
Return type:F (Array)
Raises:ValueError – if module cannot retrieve data from the AUG AFS system.
getFluxPres()[source]

returns pressure at flux surface.

Returns:[nt,npsi] array of pressure on flux surface psi.
Return type:p (Array)
Raises:ValueError – if module cannot retrieve data from AUG AFS system.
getFPrime()[source]

returns F’, often calculated for grad-shafranov solutions.

Returns:[nt,npsi] array of F=RB_{Phi}(Psi)
Return type:F (Array)
Raises:ValueError – if module cannot retrieve data from the AUG AFS system.
getFFPrime()[source]

returns FF’ function used for grad-shafranov solutions.

Returns:[nt,npsi] array of FF’ fromgrad-shafranov solution.
Return type:FFprime (Array)
Raises:ValueError – if module cannot retrieve data from the AUG AFS system.
getPPrime()[source]

returns plasma pressure gradient as a function of psi.

Returns:[nt,npsi] array of pressure gradient on flux surface psi from grad-shafranov solution.
Return type:pprime (Array)
Raises:ValueError – if module cannot retrieve data from the AUG AFS system.
getElongation()[source]

returns LCFS elongation.

Returns:[nt] array of LCFS elongation.
Return type:kappa (Array)
Raises:ValueError – if module cannot retrieve data from AFS.
getUpperTriangularity()[source]

returns LCFS upper triangularity.

Returns:[nt] array of LCFS upper triangularity.
Return type:deltau (Array)
Raises:ValueError – if module cannot retrieve data from the AUG AFS system.
getLowerTriangularity()[source]

returns LCFS lower triangularity.

Returns:[nt] array of LCFS lower triangularity.
Return type:deltal (Array)
Raises:ValueError – if module cannot retrieve data from the AUG AFS system.
getShaping()[source]

pulls LCFS elongation and upper/lower triangularity.

Returns:namedtuple containing (kappa, delta_u, delta_l)
Raises:ValueError – if module cannot retrieve data from the AUG AFS system.
getMagR(length_unit=1)[source]

returns magnetic-axis major radius.

Returns:[nt] array of major radius of magnetic axis.
Return type:magR (Array)
Raises:ValueError – if module cannot retrieve data from the AUG AFS system.
getMagZ(length_unit=1)[source]

returns magnetic-axis Z.

Returns:[nt] array of Z of magnetic axis.
Return type:magZ (Array)
Raises:ValueError – if module cannot retrieve data from the AUG AFS system.
getAreaLCFS(length_unit=2)[source]

returns LCFS cross-sectional area.

Keyword Arguments:
 length_unit (String or 2) – unit for LCFS area. Defaults to 2, denoting default areal unit (typically m^2).
Returns:[nt] array of LCFS area.
Return type:areaLCFS (Array)
Raises:ValueError – if module cannot retrieve data from the AUG AFS system.
getAOut(length_unit=1)[source]

returns outboard-midplane minor radius at LCFS.

Keyword Arguments:
 length_unit (String or 1) – unit for minor radius. Defaults to 1, denoting default length unit (typically m).
Returns:[nt] array of LCFS outboard-midplane minor radius.
Return type:aOut (Array)
Raises:ValueError – if module cannot retrieve data from the AUG AFS system.
getRmidOut(length_unit=1)[source]

returns outboard-midplane major radius.

Keyword Arguments:
 length_unit (String or 1) – unit for major radius. Defaults to 1, denoting default length unit (typically m).
Raises:NotImplementedError – Not implemented on ASDEX-Upgrade reconstructions.
getGeometry(length_unit=None)[source]

pulls dimensional geometry parameters.

Returns:namedtuple containing (magR,magZ,areaLCFS,aOut,RmidOut)
Raises:ValueError – if module cannot retrieve data from the AUG AFS system.
getQProfile()[source]

returns profile of safety factor q.

Returns:[nt,npsi] array of q on flux surface psi.
Return type:qpsi (Array)
Raises:ValueError – if module cannot retrieve data from the AUG AFS system.
getQ0()[source]

returns q on magnetic axis,q0.

Returns:[nt] array of q(psi=0).
Return type:q0 (Array)
Raises:ValueError – if module cannot retrieve data from the AUG AFS system.
getQ95()[source]

returns q at 95% flux surface.

Returns:[nt] array of q(psi=0.95).
Return type:q95 (Array)
Raises:ValueError – if module cannot retrieve data from the AUG AFS system.
getQLCFS()[source]

returns q on LCFS (interpolated).

Raises:NotImplementedError – Not implemented on ASDEX-Upgrade reconstructions.
getQ1Surf(length_unit=1)[source]

returns outboard-midplane minor radius of q=1 surface.

Raises:NotImplementedError – Not implemented on ASDEX-Upgrade reconstructions.
getQ2Surf(length_unit=1)[source]

returns outboard-midplane minor radius of q=2 surface.

Raises:NotImplementedError – Not implemented on ASDEX-Upgrade reconstructions.
getQ3Surf(length_unit=1)[source]

returns outboard-midplane minor radius of q=3 surface.

Raises:NotImplementedError – Not implemented on ASDEX-Upgrade reconstructions.
getQs(length_unit=1)[source]

pulls q values.

Raises:NotImplementedError – Not implemented on ASDEX-Upgrade reconstructions.
getBtVac()[source]

Returns vacuum toroidal field on-axis. THIS MAY BE INCORRECT

Returns:[nt] array of vacuum toroidal field.
Return type:BtVac (Array)
Raises:ValueError – if module cannot retrieve data from the AUG AFS system.
getBtPla()[source]

returns on-axis plasma toroidal field.

Raises:NotImplementedError – Not implemented on ASDEX-Upgrade reconstructions.
getBpAvg()[source]

returns average poloidal field.

Raises:NotImplementedError – Not implemented on ASDEX-Upgrade reconstructions.
getFields()[source]

pulls vacuum and plasma toroidal field, avg poloidal field.

Raises:NotImplementedError – Not implemented on ASDEX-Upgrade reconstructions.
getIpCalc()[source]

returns Plasma Current, is the same as getIpMeas.

Returns:[nt] array of the reconstructed plasma current.
Return type:IpCalc (Array)
Raises:ValueError – if module cannot retrieve data from the AUG AFS system.
getIpMeas()[source]

returns magnetics-measured plasma current.

Returns:[nt] array of measured plasma current.
Return type:IpMeas (Array)
Raises:ValueError – if module cannot retrieve data from the AUG AFS system.
getJp()[source]

returns the calculated plasma current density Jp on flux grid.

Returns:[nt,nz,nr] array of current density.
Return type:Jp (Array)
Raises:ValueError – if module cannot retrieve data from the AUG AFS system.
getBetaT()[source]

returns the calculated toroidal beta.

Raises:NotImplementedError – Not implemented on ASDEX-Upgrade reconstructions.
getBetaP()[source]

returns the calculated poloidal beta.

Returns:[nt] array of the calculated average poloidal beta.
Return type:BetaP (Array)
Raises:ValueError – if module cannot retrieve data from the AUG AFS system.
getLi()[source]

returns the calculated internal inductance.

Returns:[nt] array of the calculated internal inductance.
Return type:Li (Array)
Raises:ValueError – if module cannot retrieve data from the AUG afs system.
getBetas()[source]

pulls calculated betap, betat, internal inductance.

Raises:NotImplementedError – Not implemented on ASDEX-Upgrade reconstructions.
getDiamagFlux()[source]

returns the measured diamagnetic-loop flux.

Raises:NotImplementedError – Not implemented on ASDEX-Upgrade reconstructions.
getDiamagBetaT()[source]

returns diamagnetic-loop toroidal beta.

Raises:NotImplementedError – Not implemented on ASDEX-Upgrade reconstructions.
getDiamagBetaP()[source]

returns diamagnetic-loop avg poloidal beta.

Raises:NotImplementedError – Not implemented on ASDEX-Upgrade reconstructions.
getDiamagTauE()[source]

returns diamagnetic-loop energy confinement time.

Raises:NotImplementedError – Not implemented on ASDEX-Upgrade reconstructions.
getDiamagWp()[source]

returns diamagnetic-loop plasma stored energy.

Raises:NotImplementedError – Not implemented on ASDEX-Upgrade reconstructions.
getDiamag()[source]

pulls diamagnetic flux measurements, toroidal and poloidal beta, energy confinement time and stored energy.

Raises:NotImplementedError – Not implemented on ASDEX-Upgrade reconstructions.
getWMHD()[source]

returns calculated MHD stored energy.

Returns:[nt] array of the calculated stored energy.
Return type:WMHD (Array)
Raises:ValueError – if module cannot retrieve data from the AUG afs system.
getTauMHD()[source]

returns the calculated MHD energy confinement time.

Raises:NotImplementedError – Not implemented on ASDEX-Upgrade reconstructions.
getPinj()[source]

returns the injected power.

Raises:
  • NotImplementedError – Not implemented on ASDEX-Upgrade reconstructions.
  • –
getWbdot()[source]

returns the calculated d/dt of magnetic stored energy.

Raises:NotImplementedError – Not implemented on ASDEX-Upgrade reconstructions.
getWpdot()[source]

returns the calculated d/dt of plasma stored energy.

Raises:NotImplementedError – Not implemented on ASDEX-Upgrade reconstructions.
getBCentr()[source]

returns Vacuum toroidal magnetic field at center of plasma

Returns:[nt] array of B_t at center [T]
Return type:B_cent (Array)
Raises:ValueError – if module cannot retrieve data from the AUG afs system.
getRCentr(length_unit=1)[source]

Returns Radius of BCenter measurement

Returns:Radial position where Bcent calculated [m]
Return type:R
getEnergy()[source]

pulls the calculated energy parameters - stored energy, tau_E, injected power, d/dt of magnetic and plasma stored energy.

Raises:NotImplementedError – Not implemented on ASDEX-Upgrade reconstructions.
getMachineCrossSection()[source]

Returns R,Z coordinates of vacuum-vessel wall for masking, plotting routines.

Returns:(R_limiter, Z_limiter)
  • R_limiter (Array) - [n] array of x-values for machine cross-section.
  • Z_limiter (Array) - [n] array of y-values for machine cross-section.
getMachineCrossSectionFull()[source]

Returns R,Z coordinates of vacuum-vessel wall for plotting routines.

Absent additional vector-graphic data on machine cross-section, returns getMachineCrossSection().

Returns:result from getMachineCrossSection().
getCurrentSign()[source]

Returns the sign of the current, based on the check in Steve Wolfe’s IDL implementation efit_rz2psi.pro.

Returns:1 for positive-direction current, -1 for negative.
Return type:currentSign (Integer)
getParam(path)[source]

Backup function, applying a direct path input for tree-like data storage access for parameters not typically found in Equilbrium object. Directly calls attributes read from g/a-files in copy-safe manner.

Parameters:name (String) – Parameter name for value stored in EqdskReader instance.
Raises:NotImplementedError – Not implemented on ASDEX-Upgrade reconstructions.
getSSQ(inp, **kwargs)[source]

returns single value quantities in the case SV file doesn’t exist and coniditions the data in a way that is expected from a dd SV shotfile. This seamlessly hides the lack of an SV file.

Returns:corresponding data
Return type:signal (dd.signal Object)
Raises:ValueError – if module cannot retrieve data from the AUG AFS system.
rz2BR(R, Z, t, return_t=False, make_grid=False, each_t=True, length_unit=1)[source]

Calculates the major radial component of the magnetic field at the given (R, Z, t) coordinates.

Uses

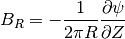
B_R = -\frac{1}{2 \pi R}\frac{\partial \psi}{\partial Z}

Parameters:
  • R (Array-like or scalar float) – Values of the radial coordinate to map to radial field. If R and Z are both scalar values, they are used as the coordinate pair for all of the values in t. Must have the same shape as Z unless the make_grid keyword is set. If the make_grid keyword is True, R must have exactly one dimension.
  • Z (Array-like or scalar float) – Values of the vertical coordinate to map to radial field. If R and Z are both scalar values, they are used as the coordinate pair for all of the values in t. Must have the same shape as R unless the make_grid keyword is set. If the make_grid keyword is True, Z must have exactly one dimension.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of R, Z. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as R and Z (or their meshgrid if make_grid is True).
Keyword Arguments:
 
  • each_t (Boolean) – When True, the elements in R, Z are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of R and Z or be a scalar. Default is True (evaluate ALL R, Z at EACH element in t).
  • make_grid (Boolean) – Set to True to pass R and Z through scipy.meshgrid() before evaluating. If this is set to True, R and Z must each only have a single dimension, but can have different lengths. Default is False (do not form meshgrid).
  • length_unit (String or 1) –

    Length unit that R, Z are given in. If a string is given, it must be a valid unit specifier:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ meters

    If length_unit is 1 or None, meters are assumed. The default value is 1 (use meters).

  • return_t (Boolean) – Set to True to return a tuple of (BR, time_idxs), where time_idxs is the array of time indices actually used in evaluating BR with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return BR).
Returns:

BR or (BR, time_idxs)

  • BR (Array or scalar float) - The major radial component of the magnetic field. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned. If R and Z both have the same shape then BR has this shape as well, unless the make_grid keyword was True, in which case BR has shape (len(Z), len(R)).
  • time_idxs (Array with same shape as BR) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single BR value at R=0.6m, Z=0.0m, t=0.26s:

BR_val = Eq_instance.rz2BR(0.6, 0, 0.26)

Find BR values at (R, Z) points (0.6m, 0m) and (0.8m, 0m) at the single time t=0.26s. Note that the Z vector must be fully specified, even if the values are all the same:

BR_arr = Eq_instance.rz2BR([0.6, 0.8], [0, 0], 0.26)

Find BR values at (R, Z) points (0.6m, 0m) at times t=[0.2s, 0.3s]:

BR_arr = Eq_instance.rz2BR(0.6, 0, [0.2, 0.3])

Find BR values at (R, Z, t) points (0.6m, 0m, 0.2s) and (0.5m, 0.2m, 0.3s):

BR_arr = Eq_instance.rz2BR([0.6, 0.5], [0, 0.2], [0.2, 0.3], each_t=False)

Find BR values on grid defined by 1D vector of radial positions R and 1D vector of vertical positions Z at time t=0.2s:

BR_mat = Eq_instance.rz2BR(R, Z, 0.2, make_grid=True)
rz2BZ(R, Z, t, return_t=False, make_grid=False, each_t=True, length_unit=1)[source]

Calculates the vertical component of the magnetic field at the given (R, Z, t) coordinates.

Uses

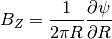
B_Z = \frac{1}{2 \pi R}\frac{\partial \psi}{\partial R}

Parameters:
  • R (Array-like or scalar float) – Values of the radial coordinate to map to vertical field. If R and Z are both scalar values, they are used as the coordinate pair for all of the values in t. Must have the same shape as Z unless the make_grid keyword is set. If the make_grid keyword is True, R must have exactly one dimension.
  • Z (Array-like or scalar float) – Values of the vertical coordinate to map to vertical field. If R and Z are both scalar values, they are used as the coordinate pair for all of the values in t. Must have the same shape as R unless the make_grid keyword is set. If the make_grid keyword is True, Z must have exactly one dimension.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of R, Z. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as R and Z (or their meshgrid if make_grid is True).
Keyword Arguments:
 
  • each_t (Boolean) – When True, the elements in R, Z are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of R and Z or be a scalar. Default is True (evaluate ALL R, Z at EACH element in t).
  • make_grid (Boolean) – Set to True to pass R and Z through scipy.meshgrid() before evaluating. If this is set to True, R and Z must each only have a single dimension, but can have different lengths. Default is False (do not form meshgrid).
  • length_unit (String or 1) –

    Length unit that R, Z are given in. If a string is given, it must be a valid unit specifier:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ meters

    If length_unit is 1 or None, meters are assumed. The default value is 1 (use meters).

  • return_t (Boolean) – Set to True to return a tuple of (BZ, time_idxs), where time_idxs is the array of time indices actually used in evaluating BZ with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return BZ).
Returns:

BZ or (BZ, time_idxs)

  • BZ (Array or scalar float) - The vertical component of the magnetic field. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned. If R and Z both have the same shape then BZ has this shape as well, unless the make_grid keyword was True, in which case BZ has shape (len(Z), len(R)).
  • time_idxs (Array with same shape as BZ) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single BZ value at R=0.6m, Z=0.0m, t=0.26s:

BZ_val = Eq_instance.rz2BZ(0.6, 0, 0.26)

Find BZ values at (R, Z) points (0.6m, 0m) and (0.8m, 0m) at the single time t=0.26s. Note that the Z vector must be fully specified, even if the values are all the same:

BZ_arr = Eq_instance.rz2BZ([0.6, 0.8], [0, 0], 0.26)

Find BZ values at (R, Z) points (0.6m, 0m) at times t=[0.2s, 0.3s]:

BZ_arr = Eq_instance.rz2BZ(0.6, 0, [0.2, 0.3])

Find BZ values at (R, Z, t) points (0.6m, 0m, 0.2s) and (0.5m, 0.2m, 0.3s):

BZ_arr = Eq_instance.rz2BZ([0.6, 0.5], [0, 0.2], [0.2, 0.3], each_t=False)

Find BZ values on grid defined by 1D vector of radial positions R and 1D vector of vertical positions Z at time t=0.2s:

BZ_mat = Eq_instance.rz2BZ(R, Z, 0.2, make_grid=True)
class eqtools.AUGData.YGCAUGInterface[source]

Bases: object

getMachineCrossSection(shot)[source]

Returns R,Z coordinates of vacuum-vessel wall for masking, plotting routines.

Returns:(R_limiter, Z_limiter)
  • R_limiter (Array) - [n] array of x-values for machine cross-section.
  • Z_limiter (Array) - [n] array of y-values for machine cross-section.
getMachineCrossSectionFull(shot)[source]

Returns R,Z coordinates of vacuum-vessel wall for plotting routines.

Absent additional vector-graphic data on machine cross-section, returns getMachineCrossSection().

Returns:result from getMachineCrossSection().
class eqtools.AUGData.AUGDDDataProp(shot, shotfile='EQH', edition=0, shotfile2=None, length_unit='m', tspline=False, monotonic=True, experiment='AUGD')[source]

Bases: eqtools.AUGData.AUGDDData, eqtools.core.PropertyAccessMixin

AUGDDData with the PropertyAccessMixin added to enable property-style access. This is good for interactive use, but may drag the performance down.

eqtools.CModEFIT module

This module provides classes inheriting eqtools.EFIT.EFITTree for working with C-Mod EFIT data.

class eqtools.CModEFIT.CModEFITTree(shot, tree='ANALYSIS', length_unit='m', gfile='g_eqdsk', afile='a_eqdsk', tspline=False, monotonic=True)[source]

Bases: eqtools.EFIT.EFITTree

Inherits eqtools.EFIT.EFITTree class. Machine-specific data handling class for Alcator C-Mod. Pulls EFIT data from selected MDS tree and shot, stores as object attributes. Each EFIT variable or set of variables is recovered with a corresponding getter method. Essential data for EFIT mapping are pulled on initialization (e.g. psirz grid). Additional data are pulled at the first request and stored for subsequent usage.

Intializes C-Mod version of EFITTree object. Pulls data from MDS tree for storage in instance attributes. Core attributes are populated from the MDS tree on initialization. Additional attributes are initialized as None, filled on the first request to the object.

Parameters:

shot (integer) – C-Mod shot index.
Keyword Arguments:
 
  • tree (string) – Optional input for EFIT tree, defaults to ‘ANALYSIS’ (i.e., EFIT data are under analysis::top.efit.results). For any string TREE (such as ‘EFIT20’) other than ‘ANALYSIS’, data are taken from TREE::top.results.
  • length_unit (string) –

    Sets the base unit used for any quantity whose dimensions are length to any power. Valid options are:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ whatever the default in the tree is (no conversion is performed, units may be inconsistent)

    Default is ‘m’ (all units taken and returned in meters).

  • gfile (string) – Optional input for EFIT geqdsk location name, defaults to ‘g_eqdsk’ (i.e., EFIT data are under tree::top.results.G_EQDSK)
  • afile (string) – Optional input for EFIT aeqdsk location name, defaults to ‘a_eqdsk’ (i.e., EFIT data are under tree::top.results.A_EQDSK)
  • tspline (Boolean) – Sets whether or not interpolation in time is performed using a tricubic spline or nearest-neighbor interpolation. Tricubic spline interpolation requires at least four complete equilibria at different times. It is also assumed that they are functionally correlated, and that parameters do not vary out of their boundaries (derivative = 0 boundary condition). Default is False (use nearest neighbor interpolation).
  • monotonic (Boolean) – Sets whether or not the “monotonic” form of time window finding is used. If True, the timebase must be monotonically increasing. Default is False (use slower, safer method).
getFluxVol(length_unit=3)[source]

returns volume within flux surface.

Keyword Arguments:
 length_unit (String or 3) – unit for plasma volume. Defaults to 3, indicating default volumetric unit (typically m^3).
Returns:[nt,npsi] array of volume within flux surface.
Return type:fluxVol (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getRmidPsi(length_unit=1)[source]

returns maximum major radius of each flux surface.

Keyword Arguments:
 length_unit (String or 1) – unit of Rmid. Defaults to 1, indicating the default parameter unit (typically m).
Returns:[nt,npsi] array of maximum (outboard) major radius of flux surface psi.
Return type:Rmid (Array)
Raises:Value Error – if module cannot retrieve data from MDS tree.
getF()[source]

returns F=RB_{Phi}(Psi), often calculated for grad-shafranov solutions.

Returns:[nt,npsi] array of F=RB_{Phi}(Psi)
Return type:F (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getFluxPres()[source]

returns pressure at flux surface.

Returns:[nt,npsi] array of pressure on flux surface psi.
Return type:p (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getFFPrime()[source]

returns FF’ function used for grad-shafranov solutions.

Returns:[nt,npsi] array of FF’ fromgrad-shafranov solution.
Return type:FFprime (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getPPrime()[source]

returns plasma pressure gradient as a function of psi.

Returns:[nt,npsi] array of pressure gradient on flux surface psi from grad-shafranov solution.
Return type:pprime (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getQProfile()[source]

returns profile of safety factor q.

Returns:[nt,npsi] array of q on flux surface psi.
Return type:qpsi (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getRLCFS(length_unit=1)[source]

returns R-values of LCFS position.

Returns:[nt,n] array of R of LCFS points.
Return type:RLCFS (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getZLCFS(length_unit=1)[source]

returns Z-values of LCFS position.

Returns:[nt,n] array of Z of LCFS points.
Return type:ZLCFS (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getMachineCrossSectionFull()[source]

Pulls C-Mod cross-section data from tree, converts to plottable vector format for use in other plotting routines

Returns:(x, y)
  • x (Array) - [n] array of x-values for machine cross-section.
  • y (Array) - [n] array of y-values for machine cross-section.
Raises:ValueError – if module cannot retrieve data from MDS tree.
getRCentr(length_unit=1)[source]

returns EFIT radius where Bcentr evaluated

Returns:Radial position where Bcent calculated [m]
Return type:R
Raises:ValueError – if module cannot retrieve data from MDS tree.
class eqtools.CModEFIT.CModEFITTreeProp(shot, tree='ANALYSIS', length_unit='m', gfile='g_eqdsk', afile='a_eqdsk', tspline=False, monotonic=True)[source]

Bases: eqtools.CModEFIT.CModEFITTree, eqtools.core.PropertyAccessMixin

CModEFITTree with the PropertyAccessMixin added to enable property-style access. This is good for interactive use, but may drag the performance down.

eqtools.D3DEFIT module

This module provides classes inheriting eqtools.EFIT.EFITTree for working with DIII-D EFIT data.

class eqtools.D3DEFIT.D3DEFITTree(shot, tree='EFIT01', length_unit='m', gfile='geqdsk', afile='aeqdsk', tspline=False, monotonic=True)[source]

Bases: eqtools.EFIT.EFITTree

Inherits eqtools.EFIT.EFITTree class. Machine-specific data handling class for DIII-D. Pulls EFIT data from selected MDS tree and shot, stores as object attributes. Each EFIT variable or set of variables is recovered with a corresponding getter method. Essential data for EFIT mapping are pulled on initialization (e.g. psirz grid). Additional data are pulled at the first request and stored for subsequent usage.

Intializes DIII-D version of EFITTree object. Pulls data from MDS tree for storage in instance attributes. Core attributes are populated from the MDS tree on initialization. Additional attributes are initialized as None, filled on the first request to the object.

Parameters:

shot (integer) – DIII-D shot index.
Keyword Arguments:
 
  • tree (string) – Optional input for EFIT tree, defaults to ‘EFIT01’ (i.e., EFIT data are under EFIT01::top.results).
  • length_unit (string) –

    Sets the base unit used for any quantity whose dimensions are length to any power. Valid options are:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ whatever the default in the tree is (no conversion is performed, units may be inconsistent)

    Default is ‘m’ (all units taken and returned in meters).

  • gfile (string) – Optional input for EFIT geqdsk location name, defaults to ‘geqdsk’ (i.e., EFIT data are under tree::top.results.GEQDSK)
  • afile (string) – Optional input for EFIT aeqdsk location name, defaults to ‘aeqdsk’ (i.e., EFIT data are under tree::top.results.AEQDSK)
  • tspline (Boolean) – Sets whether or not interpolation in time is performed using a tricubic spline or nearest-neighbor interpolation. Tricubic spline interpolation requires at least four complete equilibria at different times. It is also assumed that they are functionally correlated, and that parameters do not vary out of their boundaries (derivative = 0 boundary condition). Default is False (use nearest neighbor interpolation).
  • monotonic (Boolean) – Sets whether or not the “monotonic” form of time window finding is used. If True, the timebase must be monotonically increasing. Default is False (use slower, safer method).
getFluxVol()[source]

Not implemented in D3DEFIT tree.

Returns:volume within flux surface [psi,t]
getRmidPsi(length_unit=1)[source]

returns maximum major radius of each flux surface.

Keyword Arguments:
 length_unit (String or 1) – unit of Rmid. Defaults to 1, indicating the default parameter unit (typically m).
Returns:[nt,npsi] array of maximum (outboard) major radius of flux surface psi.
Return type:Rmid (Array)
Raises:Value Error – if module cannot retrieve data from MDS tree.
class eqtools.D3DEFIT.D3DEFITTreeProp(shot, tree='EFIT01', length_unit='m', gfile='geqdsk', afile='aeqdsk', tspline=False, monotonic=True)[source]

Bases: eqtools.D3DEFIT.D3DEFITTree, eqtools.core.PropertyAccessMixin

D3DEFITTree with the PropertyAccessMixin added to enable property-style access. This is good for interactive use, but may drag the performance down.

eqtools.EFIT module

Provides class inheriting eqtools.core.Equilibrium for working with EFIT data.

class eqtools.EFIT.EFITTree(shot, tree, root, length_unit='m', gfile='g_eqdsk', afile='a_eqdsk', tspline=False, monotonic=True)[source]

Bases: eqtools.core.Equilibrium

Inherits Equilibrium class. EFIT-specific data handling class for machines using standard EFIT tag names/tree structure with MDSplus. Constructor and/or data loading may need overriding in a machine-specific implementation. Pulls EFIT data from selected MDS tree and shot, stores as object attributes. Each EFIT variable or set of variables is recovered with a corresponding getter method. Essential data for EFIT mapping are pulled on initialization (e.g. psirz grid). Additional data are pulled at the first request and stored for subsequent usage.

Intializes EFITTree object. Pulls data from MDS tree for storage in instance attributes. Core attributes are populated from the MDS tree on initialization. Additional attributes are initialized as None, filled on the first request to the object.

Parameters:
  • shot (integer) – Shot number
  • tree (string) – MDSplus tree to open to fetch EFIT data.
  • root (string) – Root path for EFIT data in MDSplus tree.
Keyword Arguments:
 
  • length_unit (string) –

    Sets the base unit used for any quantity whose dimensions are length to any power. Valid options are:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ whatever the default in the tree is (no conversion is performed, units may be inconsistent)

    Default is ‘m’ (all units taken and returned in meters).

  • tspline (boolean) – Sets whether or not interpolation in time is performed using a tricubic spline or nearest-neighbor interpolation. Tricubic spline interpolation requires at least four complete equilibria at different times. It is also assumed that they are functionally correlated, and that parameters do not vary out of their boundaries (derivative = 0 boundary condition). Default is False (use nearest neighbor interpolation).
  • monotonic (boolean) – Sets whether or not the “monotonic” form of time window finding is used. If True, the timebase must be monotonically increasing. Default is False (use slower, safer method).
getInfo()[source]

returns namedtuple of shot information

Returns:namedtuple containing
shot C-Mod shot index (long)
tree EFIT tree (string)
nr size of R-axis for spatial grid
nz size of Z-axis for spatial grid
nt size of timebase for flux grid
getTimeBase()[source]

returns EFIT time base vector.

Returns:[nt] array of time points.
Return type:time (array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getFluxGrid()[source]

returns EFIT flux grid.

Note that this method preserves whatever sign convention is used in the tree. For C-Mod, this means that the result should be multiplied by -1 * getCurrentSign() in most cases.

Returns:[nt,nz,nr] array of (non-normalized) flux on grid.
Return type:psiRZ (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getRGrid(length_unit=1)[source]

returns EFIT R-axis.

Returns:[nr] array of R-axis of flux grid.
Return type:rGrid (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getZGrid(length_unit=1)[source]

returns EFIT Z-axis.

Returns:[nz] array of Z-axis of flux grid.
Return type:zGrid (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getFluxAxis()[source]

returns psi on magnetic axis.

Returns:[nt] array of psi on magnetic axis.
Return type:psiAxis (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getFluxLCFS()[source]

returns psi at separatrix.

Returns:[nt] array of psi at LCFS.
Return type:psiLCFS (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getFluxVol(length_unit=3)[source]

returns volume within flux surface.

Keyword Arguments:
 length_unit (String or 3) – unit for plasma volume. Defaults to 3, indicating default volumetric unit (typically m^3).
Returns:[nt,npsi] array of volume within flux surface.
Return type:fluxVol (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getVolLCFS(length_unit=3)[source]

returns volume within LCFS.

Keyword Arguments:
 length_unit (String or 3) – unit for LCFS volume. Defaults to 3, denoting default volumetric unit (typically m^3).
Returns:[nt] array of volume within LCFS.
Return type:volLCFS (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getRmidPsi(length_unit=1)[source]

returns maximum major radius of each flux surface.

Keyword Arguments:
 length_unit (String or 1) – unit of Rmid. Defaults to 1, indicating the default parameter unit (typically m).
Returns:[nt,npsi] array of maximum (outboard) major radius of flux surface psi.
Return type:Rmid (Array)
Raises:Value Error – if module cannot retrieve data from MDS tree.
getRLCFS(length_unit=1)[source]

returns R-values of LCFS position.

Returns:[nt,n] array of R of LCFS points.
Return type:RLCFS (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getZLCFS(length_unit=1)[source]

returns Z-values of LCFS position.

Returns:[nt,n] array of Z of LCFS points.
Return type:ZLCFS (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
remapLCFS(mask=False)[source]

Overwrites RLCFS, ZLCFS values pulled from EFIT with explicitly-calculated contour of psinorm=1 surface. This is then masked down by the limiter array using core.inPolygon, restricting the contour to the closed plasma surface and the divertor legs.

Keyword Arguments:
 

mask (Boolean) – Default False. Set True to mask LCFS path to limiter outline (using inPolygon). Set False to draw full contour of psi = psiLCFS.
Raises:
  • NotImplementedError – if matplotlib.pyplot is not loaded.
  • ValueError – if limiter outline is not available.
getF()[source]

returns F=RB_{Phi}(Psi), often calculated for grad-shafranov solutions.

Note that this method preserves whatever sign convention is used in the tree. For C-Mod, this means that the result should be multiplied by -1 * getCurrentSign() in most cases.

Returns:[nt,npsi] array of F=RB_{Phi}(Psi)
Return type:F (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getFluxPres()[source]

returns pressure at flux surface.

Returns:[nt,npsi] array of pressure on flux surface psi.
Return type:p (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getFFPrime()[source]

returns FF’ function used for grad-shafranov solutions.

Returns:[nt,npsi] array of FF’ fromgrad-shafranov solution.
Return type:FFprime (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getPPrime()[source]

returns plasma pressure gradient as a function of psi.

Returns:[nt,npsi] array of pressure gradient on flux surface psi from grad-shafranov solution.
Return type:pprime (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getElongation()[source]

returns LCFS elongation.

Returns:[nt] array of LCFS elongation.
Return type:kappa (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getUpperTriangularity()[source]

returns LCFS upper triangularity.

Returns:[nt] array of LCFS upper triangularity.
Return type:deltau (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getLowerTriangularity()[source]

returns LCFS lower triangularity.

Returns:[nt] array of LCFS lower triangularity.
Return type:deltal (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getShaping()[source]

pulls LCFS elongation and upper/lower triangularity.

Returns:namedtuple containing (kappa, delta_u, delta_l)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getMagR(length_unit=1)[source]

returns magnetic-axis major radius.

Returns:[nt] array of major radius of magnetic axis.
Return type:magR (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getMagZ(length_unit=1)[source]

returns magnetic-axis Z.

Returns:[nt] array of Z of magnetic axis.
Return type:magZ (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getAreaLCFS(length_unit=2)[source]

returns LCFS cross-sectional area.

Keyword Arguments:
 length_unit (String or 2) – unit for LCFS area. Defaults to 2, denoting default areal unit (typically m^2).
Returns:[nt] array of LCFS area.
Return type:areaLCFS (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getAOut(length_unit=1)[source]

returns outboard-midplane minor radius at LCFS.

Keyword Arguments:
 length_unit (String or 1) – unit for minor radius. Defaults to 1, denoting default length unit (typically m).
Returns:[nt] array of LCFS outboard-midplane minor radius.
Return type:aOut (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getRmidOut(length_unit=1)[source]

returns outboard-midplane major radius.

Keyword Arguments:
 length_unit (String or 1) – unit for major radius. Defaults to 1, denoting default length unit (typically m).
Returns:[nt] array of major radius of LCFS.
Return type:RmidOut (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getGeometry(length_unit=None)[source]

pulls dimensional geometry parameters.

Returns:namedtuple containing (magR,magZ,areaLCFS,aOut,RmidOut)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getQProfile()[source]

returns profile of safety factor q.

Returns:[nt,npsi] array of q on flux surface psi.
Return type:qpsi (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getQ0()[source]

returns q on magnetic axis,q0.

Returns:[nt] array of q(psi=0).
Return type:q0 (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getQ95()[source]

returns q at 95% flux surface.

Returns:[nt] array of q(psi=0.95).
Return type:q95 (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getQLCFS()[source]

returns q on LCFS (interpolated).

Returns:[nt] array of q* (interpolated).
Return type:qLCFS (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getQ1Surf(length_unit=1)[source]

returns outboard-midplane minor radius of q=1 surface.

Keyword Arguments:
 length_unit (String or 1) – unit for minor radius. Defaults to 1, denoting default length unit (typically m).
Returns:[nt] array of minor radius of q=1 surface.
Return type:qr1 (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getQ2Surf(length_unit=1)[source]

returns outboard-midplane minor radius of q=2 surface.

Keyword Arguments:
 length_unit (String or 1) – unit for minor radius. Defaults to 1, denoting default length unit (typically m).
Returns:[nt] array of minor radius of q=2 surface.
Return type:qr2 (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getQ3Surf(length_unit=1)[source]

returns outboard-midplane minor radius of q=3 surface.

Keyword Arguments:
 length_unit (String or 1) – unit for minor radius. Defaults to 1, denoting default length unit (typically m).
Returns:[nt] array of minor radius of q=3 surface.
Return type:qr3 (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getQs(length_unit=1)[source]

pulls q values.

Returns:namedtuple containing (q0,q95,qLCFS,rq1,rq2,rq3).
Raises:ValueError – if module cannot retrieve data from MDS tree.
getBtVac()[source]

Returns vacuum toroidal field on-axis.

Returns:[nt] array of vacuum toroidal field.
Return type:BtVac (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getBtPla()[source]

returns on-axis plasma toroidal field.

Returns:[nt] array of toroidal field including plasma effects.
Return type:BtPla (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getBpAvg()[source]

returns average poloidal field.

Returns:[nt] array of average poloidal field.
Return type:BpAvg (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getFields()[source]

pulls vacuum and plasma toroidal field, avg poloidal field.

Returns:namedtuple containing (btaxv,btaxp,bpolav).
Raises:ValueError – if module cannot retrieve data from MDS tree.
getIpCalc()[source]

returns EFIT-calculated plasma current.

Returns:[nt] array of EFIT-reconstructed plasma current.
Return type:IpCalc (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getIpMeas()[source]

returns magnetics-measured plasma current.

Returns:[nt] array of measured plasma current.
Return type:IpMeas (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getJp()[source]

returns EFIT-calculated plasma current density Jp on flux grid.

Returns:[nt,nz,nr] array of current density.
Return type:Jp (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getBetaT()[source]

returns EFIT-calculated toroidal beta.

Returns:[nt] array of EFIT-calculated average toroidal beta.
Return type:BetaT (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getBetaP()[source]

returns EFIT-calculated poloidal beta.

Returns:[nt] array of EFIT-calculated average poloidal beta.
Return type:BetaP (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getLi()[source]

returns EFIT-calculated internal inductance.

Returns:[nt] array of EFIT-calculated internal inductance.
Return type:Li (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getBetas()[source]

pulls calculated betap, betat, internal inductance

Returns:namedtuple containing (betat,betap,Li)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getDiamagFlux()[source]

returns measured diamagnetic-loop flux.

Returns:[nt] array of diamagnetic-loop flux.
Return type:Flux (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getDiamagBetaT()[source]

returns diamagnetic-loop toroidal beta.

Returns:[nt] array of measured toroidal beta.
Return type:BetaT (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getDiamagBetaP()[source]

returns diamagnetic-loop avg poloidal beta.

Returns:[nt] array of measured poloidal beta.
Return type:BetaP (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getDiamagTauE()[source]

returns diamagnetic-loop energy confinement time.

Returns:[nt] array of measured energy confinement time.
Return type:tauE (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getDiamagWp()[source]

returns diamagnetic-loop plasma stored energy.

Returns:[nt] array of measured plasma stored energy.
Return type:Wp (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getDiamag()[source]

pulls diamagnetic flux measurements, toroidal and poloidal beta, energy confinement time and stored energy.

Returns:namedtuple containing (diamag. flux, betatd, betapd, tauDiamag, WDiamag)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getWMHD()[source]

returns EFIT-calculated MHD stored energy.

Returns:[nt] array of EFIT-calculated stored energy.
Return type:WMHD (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getTauMHD()[source]

returns EFIT-calculated MHD energy confinement time.

Returns:[nt] array of EFIT-calculated energy confinement time.
Return type:tauMHD (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getPinj()[source]

returns EFIT-calculated injected power.

Returns:[nt] array of EFIT-reconstructed injected power.
Return type:Pinj (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getWbdot()[source]

returns EFIT-calculated d/dt of magnetic stored energy.

Returns:[nt] array of d(Wb)/dt
Return type:dWdt (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getWpdot()[source]

returns EFIT-calculated d/dt of plasma stored energy.

Returns:[nt] array of d(Wp)/dt
Return type:dWdt (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getBCentr()[source]

returns EFIT-Vacuum toroidal magnetic field in Tesla at Rcentr

Returns:[nt] array of B_t at center [T]
Return type:B_cent (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getRCentr(length_unit=1)[source]

returns EFIT radius where Bcentr evaluated

Returns:Radial position where Bcent calculated [m]
Return type:R
Raises:ValueError – if module cannot retrieve data from MDS tree.
getEnergy()[source]

pulls EFIT-calculated energy parameters - stored energy, tau_E, injected power, d/dt of magnetic and plasma stored energy.

Returns:namedtuple containing (WMHD,tauMHD,Pinj,Wbdot,Wpdot)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getMachineCrossSection()[source]

Returns R,Z coordinates of vacuum-vessel wall for masking, plotting routines.

Returns:(R_limiter, Z_limiter)
  • R_limiter (Array) - [n] array of x-values for machine cross-section.
  • Z_limiter (Array) - [n] array of y-values for machine cross-section.
getMachineCrossSectionFull()[source]

Returns R,Z coordinates of vacuum-vessel wall for plotting routines.

Absent additional vector-graphic data on machine cross-section, returns getMachineCrossSection().

Returns:result from getMachineCrossSection().
getCurrentSign()[source]

Returns the sign of the current, based on the check in Steve Wolfe’s IDL implementation efit_rz2psi.pro.

Returns:1 for positive-direction current, -1 for negative.
Return type:currentSign (Integer)
getParam(path)[source]

Backup function, applying a direct path input for tree-like data storage access for parameters not typically found in Equilbrium object. Directly calls attributes read from g/a-files in copy-safe manner.

Parameters:name (String) – Parameter name for value stored in EqdskReader instance.
Raises:AttributeError – raised if no attribute is found.

eqtools.FromArrays module

class eqtools.FromArrays.ArrayEquilibrium(psiRZ, rGrid, zGrid, time, q, fluxVol, psiLCFS, psiAxis, rmag, zmag, Rout, **kwargs)[source]

Bases: eqtools.core.Equilibrium

Class to represent an equilibrium specified as arrays of data.

Create ArrayEquilibrium instance from arrays of data.

Has very little checking on the shape/type of the arrays at this point.

Parameters:
  • psiRZ – Array-like, (M, N, P). Flux values at M times, N Z locations and P R locations.
  • rGrid – Array-like, (P,). R coordinates that psiRZ is given at.
  • zGrid – Array-like, (N,). Z coordinates that psiRZ is given at.
  • time – Array-like, (M,). Times that psiRZ is given at.
  • q – Array-like, (S, M). q profile evaluated at S values of psinorm from 0 to 1, given at M times.
  • fluxVol – Array-like, (S, M). Flux surface volumes evaluated at S values of psinorm from 0 to 1, given at M times.
  • psiLCFS – Array-like, (M,). Flux at the last closed flux surface, given at M times.
  • psiAxis – Array-like, (M,). Flux at the magnetic axis, given at M times.
  • rmag – Array-like, (M,). Radial coordinate of the magnetic axis, given at M times.
  • zmag – Array-like, (M,). Vertical coordinate of the magnetic axis, given at M times.
  • Rout – Outboard midplane radius of the last closed flux surface.
Keyword Arguments:
 
  • length_unit –

    String. Sets the base unit used for any quantity whose dimensions are length to any power. Valid options are:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ whatever the default in the tree is (no conversion is performed, units may be inconsistent)

    Default is ‘m’ (all units taken and returned in meters).

  • tspline – Boolean. Sets whether or not interpolation in time is performed using a tricubic spline or nearest-neighbor interpolation. Tricubic spline interpolation requires at least four complete equilibria at different times. It is also assumed that they are functionally correlated, and that parameters do not vary out of their boundaries (derivative = 0 boundary condition). Default is False (use nearest neighbor interpolation).
  • monotonic – Boolean. Sets whether or not the “monotonic” form of time window finding is used. If True, the timebase must be monotonically increasing. Default is False (use slower, safer method).
  • verbose – Boolean. Allows or blocks console readout during operation. Defaults to True, displaying useful information for the user. Set to False for quiet usage or to avoid console clutter for multiple instances.
getTimeBase()[source]

Returns a copy of the time base vector, array dimensions are (M,).

getFluxGrid()[source]

Returns a copy of the flux array, dimensions are (M, N, P), corresponding to (time, Z, R).

getRGrid(length_unit=1)[source]

Returns a copy of the radial grid, dimensions are (P,).

getZGrid(length_unit=1)[source]

Returns a copy of the vertical grid, dimensions are (N,).

getQProfile()[source]

Returns safety factor q profile (over Q values of psinorm from 0 to 1), dimensions are (Q, M)

getFluxVol(length_unit=3)[source]

returns volume within flux surface [psi,t]

getFluxLCFS()[source]

returns psi at separatrix [t]

getFluxAxis()[source]

returns psi on magnetic axis [t]

getMagR(length_unit=1)[source]

returns magnetic-axis major radius [t]

getMagZ(length_unit=1)[source]

returns magnetic-axis Z [t]

getRmidOut(length_unit=1)[source]

returns outboard-midplane major radius [t]

getRLCFS(length_unit=1)[source]

Abstract method. See child classes for implementation.

Returns R-positions (n points) mapping LCFS [t,n]

getZLCFS(length_unit=1)[source]

Abstract method. See child classes for implementation.

Returns Z-positions (n points) mapping LCFS [t,n]

getCurrentSign()[source]

Abstract method. See child classes for implementation.

Returns calculated current direction, where CCW = +

eqtools.NSTXEFIT module

This module provides classes inheriting eqtools.EFIT.EFITTree for working with NSTX EFIT data.

class eqtools.NSTXEFIT.NSTXEFITTree(shot, tree='EFIT01', length_unit='m', gfile='geqdsk', afile='aeqdsk', tspline=False, monotonic=True)[source]

Bases: eqtools.EFIT.EFITTree

Inherits EFITTree class. Machine-specific data handling class for the National Spherical Torus Experiment (NSTX). Pulls EFIT data from selected MDS tree and shot, stores as object attributes. Each EFIT variable or set of variables is recovered with a corresponding getter method. Essential data for EFIT mapping are pulled on initialization (e.g. psirz grid). Additional data are pulled at the first request and stored for subsequent usage.

Intializes NSTX version of EFITTree object. Pulls data from MDS tree for storage in instance attributes. Core attributes are populated from the MDS tree on initialization. Additional attributes are initialized as None, filled on the first request to the object.

Parameters:

shot (integer) – NSTX shot index (long)
Keyword Arguments:
 
  • tree (string) – Optional input for EFIT tree, defaults to ‘EFIT01’ (i.e., EFIT data are under EFIT01::top.results).
  • length_unit (string) –

    Sets the base unit used for any quantity whose dimensions are length to any power. Valid options are:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ whatever the default in the tree is (no conversion is performed, units may be inconsistent)

    Default is ‘m’ (all units taken and returned in meters).

  • gfile (string) – Optional input for EFIT geqdsk location name, defaults to ‘geqdsk’ (i.e., EFIT data are under tree::top.results.GEQDSK)
  • afile (string) – Optional input for EFIT aeqdsk location name, defaults to ‘aeqdsk’ (i.e., EFIT data are under tree::top.results.AEQDSK)
  • tspline (Boolean) – Sets whether or not interpolation in time is performed using a tricubic spline or nearest-neighbor interpolation. Tricubic spline interpolation requires at least four complete equilibria at different times. It is also assumed that they are functionally correlated, and that parameters do not vary out of their boundaries (derivative = 0 boundary condition). Default is False (use nearest neighbor interpolation).
  • monotonic (Boolean) – Sets whether or not the “monotonic” form of time window finding is used. If True, the timebase must be monotonically increasing. Default is False (use slower, safer method).
getFluxGrid()[source]

returns EFIT flux grid.

Returns:[nt,nz,nr] array of (non-normalized) flux on grid.
Return type:psiRZ (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getMachineCrossSection()[source]

Returns R,Z coordinates of vacuum-vessel wall for masking, plotting routines.

Returns:The requested data.
getFluxVol()[source]

Not implemented in NSTXEFIT tree.

Returns:volume within flux surface [psi,t]
getRmidPsi(length_unit=1)[source]

returns maximum major radius of each flux surface.

Keyword Arguments:
 length_unit (String or 1) – unit of Rmid. Defaults to 1, indicating the default parameter unit (typically m).
Returns:[nt,npsi] array of maximum (outboard) major radius of flux surface psi.
Return type:Rmid (Array)
Raises:Value Error – if module cannot retrieve data from MDS tree.
getIpCalc()[source]

returns EFIT-calculated plasma current.

Returns:[nt] array of EFIT-reconstructed plasma current.
Return type:IpCalc (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getVolLCFS(length_unit=3)[source]

returns volume within LCFS.

Keyword Arguments:
 length_unit (String or 3) – unit for LCFS volume. Defaults to 3, denoting default volumetric unit (typically m^3).
Returns:[nt] array of volume within LCFS.
Return type:volLCFS (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getJp()[source]

Not implemented in NSTXEFIT tree.

Returns:EFIT-calculated plasma current density Jp on flux grid [t,r,z]
rz2volnorm(*args, **kwargs)[source]

Calculated normalized volume of flux surfaces not stored in NSTX EFIT.

Returns:All mapping with Volnorm not implemented
psinorm2volnorm(*args, **kwargs)[source]

Calculated normalized volume of flux surfaces not stored in NSTX EFIT.

Returns:All maping with Volnorm not implemented
class eqtools.NSTXEFIT.NSTXEFITTreeProp(shot, tree='EFIT01', length_unit='m', gfile='geqdsk', afile='aeqdsk', tspline=False, monotonic=True)[source]

Bases: eqtools.NSTXEFIT.NSTXEFITTree, eqtools.core.PropertyAccessMixin

NSTXEFITTree with the PropertyAccessMixin added to enable property-style access. This is good for interactive use, but may drag the performance down.

eqtools.TCVLIUQE module

This module provides classes inheriting eqtools.EFIT.EFITTree for working with TCV LIUQE Equilibrium.

eqtools.TCVLIUQE.greenArea(vs)[source]
class eqtools.TCVLIUQE.TCVLIUQETree(shot, tree='tcv_shot', length_unit='m', gfile='g_eqdsk', afile='a_eqdsk', tspline=False, monotonic=True)[source]

Bases: eqtools.EFIT.EFITTree

Inherits eqtools.EFIT.EFITTree class. Machine-specific data handling class for TCV Machine. Pulls LIUQUE data from selected MDS tree and shot, stores as object attributes eventually transforming it in the equivalent quantity for EFIT. Each variable or set of variables is recovered with a corresponding getter method. Essential data for LIUQUE mapping are pulled on initialization (e.g. psirz grid). Additional data are pulled at the first request and stored for subsequent usage.

Intializes TCV version of EFITTree object. Pulls data from MDS tree for storage in instance attributes. Core attributes are populated from the MDS tree on initialization. Additional attributes are initialized as None, filled on the first request to the object.

Parameters:

shot (integer) – TCV shot index.
Keyword Arguments:
 
  • tree (string) – Optional input for LIUQE tree, defaults to ‘RESULTS’ (i.e., LIUQE data are under results::).
  • length_unit (string) –

    Sets the base unit used for any quantity whose dimensions are length to any power. Valid options are:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ whatever the default in the tree is (no conversion is performed, units may be inconsistent)

    Default is ‘m’ (all units taken and returned in meters).

  • gfile (string) – Optional input for EFIT geqdsk location name, defaults to ‘g_eqdsk’ (i.e., EFIT data are under tree::top.results.G_EQDSK)
  • afile (string) – Optional input for EFIT aeqdsk location name, defaults to ‘a_eqdsk’ (i.e., EFIT data are under tree::top.results.A_EQDSK)
  • tspline (Boolean) – Sets whether or not interpolation in time is performed using a tricubic spline or nearest-neighbor interpolation. Tricubic spline interpolation requires at least four complete equilibria at different times. It is also assumed that they are functionally correlated, and that parameters do not vary out of their boundaries (derivative = 0 boundary condition). Default is False (use nearest neighbor interpolation).
  • monotonic (Boolean) – Sets whether or not the “monotonic” form of time window finding is used. If True, the timebase must be monotonically increasing. Default is False (use slower, safer method).
getInfo()[source]

returns namedtuple of shot information

Returns:namedtuple containing
shot TCV shot index (long)
tree LIUQE tree (string)
nr size of R-axis for spatial grid
nz size of Z-axis for spatial grid
nt size of timebase for flux grid
getTimeBase()[source]

returns LIUQE time base vector.

Returns:[nt] array of time points.
Return type:time (array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getFluxGrid()[source]

returns LIUQE flux grid.

Returns:[nt,nz,nr] array of (non-normalized) flux on grid.
Return type:psiRZ (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getRGrid(length_unit=1)[source]

returns LIUQE R-axis.

Returns:[nr] array of R-axis of flux grid.
Return type:rGrid (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getZGrid(length_unit=1)[source]

returns LIUQE Z-axis.

Returns:[nz] array of Z-axis of flux grid.
Return type:zGrid (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getFluxAxis()[source]

returns psi on magnetic axis.

Returns:[nt] array of psi on magnetic axis.
Return type:psiAxis (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getFluxLCFS()[source]

returns psi at separatrix.

Returns:[nt] array of psi at LCFS.
Return type:psiLCFS (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getFluxVol(length_unit=3)[source]

returns volume within flux surface. This is not implemented in LIUQE as default output. So we use contour and GREEN theorem to get the area within a default grid of the PSI. Then we compute the volume by multipling for 2pi * VolLCFS / AreaLCFS.

Keyword Arguments:
 length_unit (String or 3) – unit for plasma volume. Defaults to 3, indicating default volumetric unit (typically m^3).
Returns:[nt,npsi] array of volume within flux surface.
Return type:fluxVol (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getVolLCFS(length_unit=3)[source]

returns volume within LCFS.

Keyword Arguments:
 length_unit (String or 3) – unit for LCFS volume. Defaults to 3, denoting default volumetric unit (typically m^3).
Returns:[nt] array of volume within LCFS.
Return type:volLCFS (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getRmidPsi(length_unit=1)[source]

returns maximum major radius of each flux surface.

Keyword Arguments:
 length_unit (String or 1) – unit of Rmid. Defaults to 1, indicating the default parameter unit (typically m).
Returns:[nt,npsi] array of maximum (outboard) major radius of flux surface psi.
Return type:Rmid (Array)
Raises:Value Error – if module cannot retrieve data from MDS tree.
getRLCFS(length_unit=1)[source]

returns R-values of LCFS position.

Returns:[nt,n] array of R of LCFS points.
Return type:RLCFS (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getZLCFS(length_unit=1)[source]

returns Z-values of LCFS position.

Returns:[nt,n] array of Z of LCFS points.
Return type:ZLCFS (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getF()[source]

returns F=RB_{Phi}(Psi), often calculated for grad-shafranov solutions. Not implemented on LIUQE

Returns:[nt,npsi] array of F=RB_{Phi}(Psi) Not stored on LIUQE nodes
Return type:F (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getFluxPres()[source]
returns pressure at flux surface. Not implemented. We have pressure
saved on the same grid of psi
Returns:[nt,npsi] array of pressure on flux surface psi. Not implemented on LIUQE nodes. We have pressure on the grid use for psi
Return type:p (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getFFPrime()[source]

returns FF’ function used for grad-shafranov solutions.

Returns:[nt,npsi] array of FF’ fromgrad-shafranov solution.
Return type:FFprime (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getPPrime()[source]

returns plasma pressure gradient as a function of psi.

Returns:[nt,npsi] array of pressure gradient on flux surface psi from grad-shafranov solution.
Return type:pprime (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getElongation()[source]

returns LCFS elongation.

Returns:[nt] array of LCFS elongation.
Return type:kappa (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getUpperTriangularity()[source]

returns LCFS upper triangularity.

Returns:[nt] array of LCFS upper triangularity.
Return type:deltau (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getLowerTriangularity()[source]

returns LCFS lower triangularity.

Returns:[nt] array of LCFS lower triangularity.
Return type:deltal (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getMagR(length_unit=1)[source]

returns magnetic-axis major radius.

Returns:[nt] array of major radius of magnetic axis.
Return type:magR (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getMagZ(length_unit=1)[source]

returns magnetic-axis Z.

Returns:[nt] array of Z of magnetic axis.
Return type:magZ (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getAreaLCFS(length_unit=2)[source]

returns LCFS cross-sectional area.

Keyword Arguments:
 length_unit (String or 2) – unit for LCFS area. Defaults to 2, denoting default areal unit (typically m^2).
Returns:[nt] array of LCFS area.
Return type:areaLCFS (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getAOut(length_unit=1)[source]
returns outboard-midplane minor radius at LCFS. In LIUQE it is the last value
of

esults::r_max_psi

Keyword Args:
length_unit (String or 1): unit for minor radius. Defaults to 1,
denoting default length unit (typically m).
Returns:
aOut (Array): [nt] array of LCFS outboard-midplane minor radius.
Raises:
ValueError: if module cannot retrieve data from MDS tree.
getRmidOut(length_unit=1)[source]

returns outboard-midplane major radius. It uses getA

Keyword Arguments:
 length_unit (String or 1) – unit for major radius. Defaults to 1, denoting default length unit (typically m).
Returns:[nt] array of major radius of LCFS.
Return type:RmidOut (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getQProfile()[source]

returns profile of safety factor q.

Returns:[nt,npsi] array of q on flux surface psi.
Return type:qpsi (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getQ0()[source]

returns q on magnetic axis,q0.

Returns:[nt] array of q(psi=0).
Return type:q0 (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getQ95()[source]

returns q at 95% flux surface.

Returns:[nt] array of q(psi=0.95).
Return type:q95 (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getQLCFS()[source]

returns q on LCFS (interpolated).

Returns:[nt] array of q* (interpolated).
Return type:qLCFS (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getBtVac()[source]

Returns vacuum toroidal field on-axis. We use MDSplus.Connection for a proper use of the TDI function tcv_eq()

Returns:[nt] array of vacuum toroidal field.
Return type:BtVac (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getBtPla()[source]

returns on-axis plasma toroidal field.

Returns:[nt] array of toroidal field including plasma effects.
Return type:BtPla (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getIpCalc()[source]

returns EFIT-calculated plasma current.

Returns:[nt] array of EFIT-reconstructed plasma current.
Return type:IpCalc (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getIpMeas()[source]

returns magnetics-measured plasma current.

Returns:[nt] array of measured plasma current.
Return type:IpMeas (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getBetaT()[source]

returns LIUQE-calculated toroidal beta.

Returns:[nt] array of LIUQE-calculated average toroidal beta.
Return type:BetaT (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getBetaP()[source]

returns LIUQE-calculated poloidal beta.

Returns:[nt] array of LIUQE-calculated average poloidal beta.
Return type:BetaP (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getLi()[source]

returns LIUQE-calculated internal inductance.

Returns:[nt] array of LIUQE-calculated internal inductance.
Return type:Li (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getDiamagWp()[source]

returns diamagnetic-loop plasma stored energy.

Returns:[nt] array of measured plasma stored energy.
Return type:Wp (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getTauMHD()[source]

returns LIUQE-calculated MHD energy confinement time.

Returns:[nt] array of LIUQE-calculated energy confinement time.
Return type:tauMHD (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getMachineCrossSection()[source]

Pulls TCV cross-section data from tree, converts to plottable vector format for use in other plotting routines

Returns:(x, y)
  • x (Array) - [n] array of x-values for machine cross-section.
  • y (Array) - [n] array of y-values for machine cross-section.
Raises:ValueError – if module cannot retrieve data from MDS tree.
getMachineCrossSectionPatch()[source]

Pulls TCV cross-section data from tree, converts it directly to a matplotlib patch which can be simply added to the approriate axes call in plotFlux()

Returns:tiles matplotlib Patch, vessel matplotlib Patch
Raises:ValueError – if module cannot retrieve data from MDS tree.
plotFlux(fill=True, mask=False)[source]

Plots LIQUE TCV flux contours directly from psi grid.

Returns the Figure instance created and the time slider widget (in case you need to modify the callback). f.axes contains the contour plot as the first element and the time slice slider as the second element.

Keyword Arguments:
 fill (Boolean) – Set True to plot filled contours. Set False (default) to plot white-background color contours.
class eqtools.TCVLIUQE.TCVLIUQETreeProp(shot, tree='tcv_shot', length_unit='m', gfile='g_eqdsk', afile='a_eqdsk', tspline=False, monotonic=True)[source]

Bases: eqtools.TCVLIUQE.TCVLIUQETree, eqtools.core.PropertyAccessMixin

TCVLIUQETree with the PropertyAccessMixin added to enable property-style access. This is good for interactive use, but may drag the performance down.

eqtools.afilereader module

This module contains the AFileReader class, a lightweight data handler for a-file (time-history) datasets.

Classes:
AFileReader:
Data-storage class for a-file data. Reads data from ASCII a-file, storing as copy-safe object attributes.
class eqtools.afilereader.AFileReader(afile)[source]

Bases: object

Class to read ASCII a-file (time-history data storage) into lightweight, user-friendly data structure.

A-files store data blocks of scalar time-history data for EFIT plasma equilibrium. Each parameter is read into a pseudo-private object attribute (marked by a leading underscore), followed by the standard EFIT variable names.

initialize object, reading from file.

Parameters:afile (String) – file path to a-file

Examples

Load a-file data located at file_path:

afr = eqtools.AFileReader(file_path)

Recover a datapoint (for example, shot, stored as afr._shot), using copy-protected __getattribute__ method:

shot = afr.shot

Assign a new attribute to afr – note that this will raise an AttributeError if attempting to overwrite a previously-stored attribute:

afr.attribute = val

eqtools.core module

This module provides the core classes for eqtools, including the base Equilibrium class.

exception eqtools.core.ModuleWarning[source]

Bases: exceptions.Warning

Warning class to notify the user of unavailable modules.

class eqtools.core.PropertyAccessMixin[source]

Bases: object

Mixin to implement access of getter methods through a property-type interface without the need to apply a decorator to every property.

For any getter obj.getSomething(), the call obj.Something will do the same thing.

This is accomplished by overriding __getattribute__() such that if an attribute ATTR does not exist it then attempts to call self.getATTR(). If self.getATTR() does not exist, an AttributeError will be raised as usual.

Also overrides __setattr__() such that it will raise an AttributeError when attempting to write an attribute ATTR for which there is already a method getATTR.

eqtools.core.inPolygon(polyx, polyy, pointx, pointy)[source]

Function calculating whether a given point is within a 2D polygon.

Given an array of X,Y coordinates describing a 2D polygon, checks whether a point given by x,y coordinates lies within the polygon. Operates via a ray-casting approach - the function projects a semi-infinite ray parallel to the positive horizontal axis, and counts how many edges of the polygon this ray intersects. For a simply-connected polygon, this determines whether the point is inside (even number of crossings) or outside (odd number of crossings) the polygon, by the Jordan Curve Theorem.

Parameters:
  • polyx (Array-like) – Array of x-coordinates of the vertices of the polygon.
  • polyy (Array-like) – Array of y-coordinates of the vertices of the polygon.
  • pointx (Int or float) – x-coordinate of test point.
  • pointy (Int or float) – y-coordinate of test point.
Returns:

True/False result for whether the point is contained within the polygon.
Return type:

result (Boolean)
class eqtools.core.Equilibrium(length_unit='m', tspline=False, monotonic=True, verbose=True)[source]

Bases: object

Abstract class of data handling object for magnetic reconstruction outputs.

Defines the mapping routines and method fingerprints necessary. Each variable or set of variables is recovered with a corresponding getter method. Essential data for mapping are pulled on initialization (psirz grid, for example) to frontload overhead. Additional data are pulled at the first request and stored for subsequent usage.

Note

This abstract class should not be used directly. Device- and code- specific subclasses are set up to account for inter-device/-code differences in data storage.

Keyword Arguments:
 
  • length_unit (String) –

    Sets the base unit used for any quantity whose dimensions are length to any power. Valid options are:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ whatever the default in the tree is (no conversion is performed, units may be inconsistent)

    Default is ‘m’ (all units taken and returned in meters).

  • tspline (Boolean) – Sets whether or not interpolation in time is performed using a tricubic spline or nearest-neighbor interpolation. Tricubic spline interpolation requires at least four complete equilibria at different times. It is also assumed that they are functionally correlated, and that parameters do not vary out of their boundaries (derivative = 0 boundary condition). Default is False (use nearest-neighbor interpolation).
  • monotonic (Boolean) – Sets whether or not the “monotonic” form of time window finding is used. If True, the timebase must be monotonically increasing. Default is False (use slower, safer method).
  • verbose (Boolean) – Allows or blocks console readout during operation. Defaults to True, displaying useful information for the user. Set to False for quiet usage or to avoid console clutter for multiple instances.
Raises:
  • ValueError – If length_unit is not a valid unit specifier.
  • ValueError – If tspline is True but module trispline did not load successfully.
rho2rho(origin, destination, *args, **kwargs)[source]

Convert from one coordinate to another.

Parameters:
  • origin (String) –

    Indicates which coordinates the data are given in. Valid options are:

    RZ R,Z coordinates
    psinorm Normalized poloidal flux
    phinorm Normalized toroidal flux
    volnorm Normalized volume
    Rmid Midplane major radius
    r/a Normalized minor radius

    Additionally, each valid option may be prepended with ‘sqrt’ to specify the square root of the desired unit.

  • destination (String) –

    Indicates which coordinates to convert to. Valid options are:

    psinorm Normalized poloidal flux
    phinorm Normalized toroidal flux
    volnorm Normalized volume
    Rmid Midplane major radius
    r/a Normalized minor radius
    q Safety factor
    F Flux function 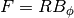F=RB_{\phi}
    FFPrime Flux function 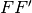FF'
    p Pressure
    pprime Pressure gradient
    v Flux surface volume

    Additionally, each valid option may be prepended with ‘sqrt’ to specify the square root of the desired unit.

  • rho (Array-like or scalar float) – Values of the starting coordinate to map to the new coordinate. Will be two arguments R, Z if origin is ‘RZ’.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of rho. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as rho (or the meshgrid of R and Z if make_grid is True).
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of rho. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in rho are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of rho or be a scalar. Default is True (evaluate ALL rho at EACH element in t).
  • make_grid (Boolean) – Only applicable if origin is ‘RZ’. Set to True to pass R and Z through scipy.meshgrid() before evaluating. If this is set to True, R and Z must each only have a single dimension, but can have different lengths. Default is False (do not form meshgrid).
  • rho (Boolean) – Set to True to return r/a (normalized minor radius) instead of Rmid when destination is Rmid. Default is False (return major radius, Rmid).
  • length_unit (String or 1) –

    Length unit that quantities are given/returned in, as applicable. If a string is given, it must be a valid unit specifier:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ meters

    If length_unit is 1 or None, meters are assumed. The default value is 1 (use meters).

  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • return_t (Boolean) – Set to True to return a tuple of (rho, time_idxs), where time_idxs is the array of time indices actually used in evaluating rho with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return rho).
Returns:

rho or (rho, time_idxs)

  • rho (Array or scalar float) - The converted coordinates. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as rho) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.
Raises:

ValueError – If origin is not one of the supported values.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single psinorm value at r/a=0.6, t=0.26s:

psi_val = Eq_instance.rho2rho('r/a', 'psinorm', 0.6, 0.26)

Find psinorm values at r/a points 0.6 and 0.8 at the single time t=0.26s:

psi_arr = Eq_instance.rho2rho('r/a', 'psinorm', [0.6, 0.8], 0.26)

Find psinorm values at r/a of 0.6 at times t=[0.2s, 0.3s]:

psi_arr = Eq_instance.rho2rho('r/a', 'psinorm', 0.6, [0.2, 0.3])

Find psinorm values at (r/a, t) points (0.6, 0.2s) and (0.5, 0.3s):

psi_arr = Eq_instance.rho2rho('r/a', 'psinorm', [0.6, 0.5], [0.2, 0.3], each_t=False)
rz2psi(R, Z, t, return_t=False, make_grid=False, each_t=True, length_unit=1)[source]

Converts the passed R, Z, t arrays to psi (unnormalized poloidal flux) values.

What is usually returned by EFIT is the stream function, 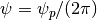\psi=\psi_p/(2\pi) which has units of Wb/rad.

Parameters:
  • R (Array-like or scalar float) – Values of the radial coordinate to map to poloidal flux. If R and Z are both scalar values, they are used as the coordinate pair for all of the values in t. Must have the same shape as Z unless the make_grid keyword is set. If the make_grid keyword is True, R must have exactly one dimension.
  • Z (Array-like or scalar float) – Values of the vertical coordinate to map to poloidal flux. If R and Z are both scalar values, they are used as the coordinate pair for all of the values in t. Must have the same shape as R unless the make_grid keyword is set. If the make_grid keyword is True, Z must have exactly one dimension.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of R, Z. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as R and Z (or their meshgrid if make_grid is True).
Keyword Arguments:
 
  • each_t (Boolean) – When True, the elements in R, Z are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of R and Z or be a scalar. Default is True (evaluate ALL R, Z at EACH element in t).
  • make_grid (Boolean) – Set to True to pass R and Z through scipy.meshgrid() before evaluating. If this is set to True, R and Z must each only have a single dimension, but can have different lengths. Default is False (do not form meshgrid).
  • length_unit (String or 1) –

    Length unit that R, Z are given in. If a string is given, it must be a valid unit specifier:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ meters

    If length_unit is 1 or None, meters are assumed. The default value is 1 (use meters).

  • return_t (Boolean) – Set to True to return a tuple of (rho, time_idxs), where time_idxs is the array of time indices actually used in evaluating rho with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return rho).
Returns:

psi or (psi, time_idxs)

  • psi (Array or scalar float) - The unnormalized poloidal flux. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned. If R and Z both have the same shape then psi has this shape as well, unless the make_grid keyword was True, in which case psi has shape (len(Z), len(R)).
  • time_idxs (Array with same shape as psi) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single psi value at R=0.6m, Z=0.0m, t=0.26s:

psi_val = Eq_instance.rz2psi(0.6, 0, 0.26)

Find psi values at (R, Z) points (0.6m, 0m) and (0.8m, 0m) at the single time t=0.26s. Note that the Z vector must be fully specified, even if the values are all the same:

psi_arr = Eq_instance.rz2psi([0.6, 0.8], [0, 0], 0.26)

Find psi values at (R, Z) points (0.6m, 0m) at times t=[0.2s, 0.3s]:

psi_arr = Eq_instance.rz2psi(0.6, 0, [0.2, 0.3])

Find psi values at (R, Z, t) points (0.6m, 0m, 0.2s) and (0.5m, 0.2m, 0.3s):

psi_arr = Eq_instance.rz2psi([0.6, 0.5], [0, 0.2], [0.2, 0.3], each_t=False)

Find psi values on grid defined by 1D vector of radial positions R and 1D vector of vertical positions Z at time t=0.2s:

psi_mat = Eq_instance.rz2psi(R, Z, 0.2, make_grid=True)
rz2psinorm(R, Z, t, return_t=False, sqrt=False, make_grid=False, each_t=True, length_unit=1)[source]

Calculates the normalized poloidal flux at the given (R, Z, t).

Uses the definition:

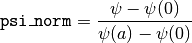
\texttt{psi\_norm} = \frac{\psi - \psi(0)}{\psi(a) - \psi(0)}

Parameters:
  • R (Array-like or scalar float) – Values of the radial coordinate to map to psinorm. If R and Z are both scalar values, they are used as the coordinate pair for all of the values in t. Must have the same shape as Z unless the make_grid keyword is set. If the make_grid keyword is True, R must have exactly one dimension.
  • Z (Array-like or scalar float) – Values of the vertical coordinate to map to psinorm. If R and Z are both scalar values, they are used as the coordinate pair for all of the values in t. Must have the same shape as R unless the make_grid keyword is set. If the make_grid keyword is True, Z must have exactly one dimension.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of R, Z. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as R and Z (or their meshgrid if make_grid is True).
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of psinorm. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in R, Z are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of R and Z or be a scalar. Default is True (evaluate ALL R, Z at EACH element in t).
  • make_grid (Boolean) – Set to True to pass R and Z through scipy.meshgrid() before evaluating. If this is set to True, R and Z must each only have a single dimension, but can have different lengths. Default is False (do not form meshgrid).
  • length_unit (String or 1) –

    Length unit that R, Z are given in. If a string is given, it must be a valid unit specifier:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ meters

    If length_unit is 1 or None, meters are assumed. The default value is 1 (use meters).

  • return_t (Boolean) – Set to True to return a tuple of (rho, time_idxs), where time_idxs is the array of time indices actually used in evaluating rho with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return rho).
Returns:

psinorm or (psinorm, time_idxs)

  • psinorm (Array or scalar float) - The normalized poloidal flux. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned. If R and Z both have the same shape then psinorm has this shape as well, unless the make_grid keyword was True, in which case psinorm has shape (len(Z), len(R)).
  • time_idxs (Array with same shape as psinorm) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single psinorm value at R=0.6m, Z=0.0m, t=0.26s:

psi_val = Eq_instance.rz2psinorm(0.6, 0, 0.26)

Find psinorm values at (R, Z) points (0.6m, 0m) and (0.8m, 0m) at the single time t=0.26s. Note that the Z vector must be fully specified, even if the values are all the same:

psi_arr = Eq_instance.rz2psinorm([0.6, 0.8], [0, 0], 0.26)

Find psinorm values at (R, Z) points (0.6m, 0m) at times t=[0.2s, 0.3s]:

psi_arr = Eq_instance.rz2psinorm(0.6, 0, [0.2, 0.3])

Find psinorm values at (R, Z, t) points (0.6m, 0m, 0.2s) and (0.5m, 0.2m, 0.3s):

psi_arr = Eq_instance.rz2psinorm([0.6, 0.5], [0, 0.2], [0.2, 0.3], each_t=False)

Find psinorm values on grid defined by 1D vector of radial positions R and 1D vector of vertical positions Z at time t=0.2s:

psi_mat = Eq_instance.rz2psinorm(R, Z, 0.2, make_grid=True)
rz2phinorm(*args, **kwargs)[source]

Calculates the normalized toroidal flux.

Uses the definitions:

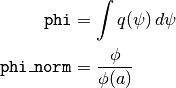
\texttt{phi} &= \int q(\psi)\,d\psi\\ \texttt{phi\_norm} &= \frac{\phi}{\phi(a)}

This is based on the IDL version efit_rz2rho.pro by Steve Wolfe.

Parameters:
  • R (Array-like or scalar float) – Values of the radial coordinate to map to phinorm. If R and Z are both scalar values, they are used as the coordinate pair for all of the values in t. Must have the same shape as Z unless the make_grid keyword is set. If the make_grid keyword is True, R must have exactly one dimension.
  • Z (Array-like or scalar float) – Values of the vertical coordinate to map to phinorm. If R and Z are both scalar values, they are used as the coordinate pair for all of the values in t. Must have the same shape as R unless the make_grid keyword is set. If the make_grid keyword is True, Z must have exactly one dimension.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of R, Z. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as R and Z (or their meshgrid if make_grid is True).
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of phinorm. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in R, Z are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of R and Z or be a scalar. Default is True (evaluate ALL R, Z at EACH element in t).
  • make_grid (Boolean) – Set to True to pass R and Z through scipy.meshgrid() before evaluating. If this is set to True, R and Z must each only have a single dimension, but can have different lengths. Default is False (do not form meshgrid).
  • length_unit (String or 1) –

    Length unit that R, Z are given in. If a string is given, it must be a valid unit specifier:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ meters

    If length_unit is 1 or None, meters are assumed. The default value is 1 (use meters).

  • k (positive int) – The degree of polynomial spline interpolation to use in converting psinorm to phinorm.
  • return_t (Boolean) – Set to True to return a tuple of (rho, time_idxs), where time_idxs is the array of time indices actually used in evaluating rho with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return rho).
Returns:

phinorm or (phinorm, time_idxs)

  • phinorm (Array or scalar float) - The normalized toroidal flux. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned. If R and Z both have the same shape then phinorm has this shape as well, unless the make_grid keyword was True, in which case phinorm has shape (len(Z), len(R)).
  • time_idxs (Array with same shape as phinorm) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single phinorm value at R=0.6m, Z=0.0m, t=0.26s:

phi_val = Eq_instance.rz2phinorm(0.6, 0, 0.26)

Find phinorm values at (R, Z) points (0.6m, 0m) and (0.8m, 0m) at the single time t=0.26s. Note that the Z vector must be fully specified, even if the values are all the same:

phi_arr = Eq_instance.rz2phinorm([0.6, 0.8], [0, 0], 0.26)

Find phinorm values at (R, Z) points (0.6m, 0m) at times t=[0.2s, 0.3s]:

phi_arr = Eq_instance.rz2phinorm(0.6, 0, [0.2, 0.3])

Find phinorm values at (R, Z, t) points (0.6m, 0m, 0.2s) and (0.5m, 0.2m, 0.3s):

phi_arr = Eq_instance.rz2phinorm([0.6, 0.5], [0, 0.2], [0.2, 0.3], each_t=False)

Find phinorm values on grid defined by 1D vector of radial positions R and 1D vector of vertical positions Z at time t=0.2s:

phi_mat = Eq_instance.rz2phinorm(R, Z, 0.2, make_grid=True)
rz2volnorm(*args, **kwargs)[source]

Calculates the normalized flux surface volume.

Based on the IDL version efit_rz2rho.pro by Steve Wolfe.

Parameters:
  • R (Array-like or scalar float) – Values of the radial coordinate to map to volnorm. If R and Z are both scalar values, they are used as the coordinate pair for all of the values in t. Must have the same shape as Z unless the make_grid keyword is set. If the make_grid keyword is True, R must have exactly one dimension.
  • Z (Array-like or scalar float) – Values of the vertical coordinate to map to volnorm. If R and Z are both scalar values, they are used as the coordinate pair for all of the values in t. Must have the same shape as R unless the make_grid keyword is set. If the make_grid keyword is True, Z must have exactly one dimension.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of R, Z. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as R and Z (or their meshgrid if make_grid is True).
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of volnorm. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in R, Z are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of R and Z or be a scalar. Default is True (evaluate ALL R, Z at EACH element in t).
  • make_grid (Boolean) – Set to True to pass R and Z through scipy.meshgrid() before evaluating. If this is set to True, R and Z must each only have a single dimension, but can have different lengths. Default is False (do not form meshgrid).
  • length_unit (String or 1) –

    Length unit that R, Z are given in. If a string is given, it must be a valid unit specifier:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ meters

    If length_unit is 1 or None, meters are assumed. The default value is 1 (use meters).

  • k (positive int) – The degree of polynomial spline interpolation to use in converting psinorm to volnorm.
  • return_t (Boolean) – Set to True to return a tuple of (rho, time_idxs), where time_idxs is the array of time indices actually used in evaluating rho with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return rho).
Returns:

volnorm or (volnorm, time_idxs)

  • volnorm (Array or scalar float) - The normalized volume. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned. If R and Z both have the same shape then volnorm has this shape as well, unless the make_grid keyword was True, in which case volnorm has shape (len(Z), len(R)).
  • time_idxs (Array with same shape as volnorm) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single volnorm value at R=0.6m, Z=0.0m, t=0.26s:

psi_val = Eq_instance.rz2volnorm(0.6, 0, 0.26)

Find volnorm values at (R, Z) points (0.6m, 0m) and (0.8m, 0m) at the single time t=0.26s. Note that the Z vector must be fully specified, even if the values are all the same:

vol_arr = Eq_instance.rz2volnorm([0.6, 0.8], [0, 0], 0.26)

Find volnorm values at (R, Z) points (0.6m, 0m) at times t=[0.2s, 0.3s]:

vol_arr = Eq_instance.rz2volnorm(0.6, 0, [0.2, 0.3])

Find volnorm values at (R, Z, t) points (0.6m, 0m, 0.2s) and (0.5m, 0.2m, 0.3s):

vol_arr = Eq_instance.rz2volnorm([0.6, 0.5], [0, 0.2], [0.2, 0.3], each_t=False)

Find volnorm values on grid defined by 1D vector of radial positions R and 1D vector of vertical positions Z at time t=0.2s:

vol_mat = Eq_instance.rz2volnorm(R, Z, 0.2, make_grid=True)
rz2rmid(*args, **kwargs)[source]

Maps the given points to the outboard midplane major radius, Rmid.

Based on the IDL version efit_rz2rmid.pro by Steve Wolfe.

Parameters:
  • R (Array-like or scalar float) – Values of the radial coordinate to map to Rmid. If R and Z are both scalar values, they are used as the coordinate pair for all of the values in t. Must have the same shape as Z unless the make_grid keyword is set. If the make_grid keyword is True, R must have exactly one dimension.
  • Z (Array-like or scalar float) – Values of the vertical coordinate to map to Rmid. If R and Z are both scalar values, they are used as the coordinate pair for all of the values in t. Must have the same shape as R unless the make_grid keyword is set. If the make_grid keyword is True, Z must have exactly one dimension.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of R, Z. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as R and Z (or their meshgrid if make_grid is True).
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of Rmid. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in R, Z are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of R and Z or be a scalar. Default is True (evaluate ALL R, Z at EACH element in t).
  • make_grid (Boolean) – Set to True to pass R and Z through scipy.meshgrid() before evaluating. If this is set to True, R and Z must each only have a single dimension, but can have different lengths. Default is False (do not form meshgrid).
  • rho (Boolean) – Set to True to return r/a (normalized minor radius) instead of Rmid. Default is False (return major radius, Rmid).
  • length_unit (String or 1) –

    Length unit that R, Z are given in, AND that Rmid is returned in. If a string is given, it must be a valid unit specifier:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ meters

    If length_unit is 1 or None, meters are assumed. The default value is 1 (use meters).

  • k (positive int) – The degree of polynomial spline interpolation to use in converting psinorm to Rmid.
  • return_t (Boolean) – Set to True to return a tuple of (rho, time_idxs), where time_idxs is the array of time indices actually used in evaluating rho with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return rho).
Returns:

Rmid or (Rmid, time_idxs)

  • Rmid (Array or scalar float) - The outboard midplan major radius. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned. If R and Z both have the same shape then Rmid has this shape as well, unless the make_grid keyword was True, in which case Rmid has shape (len(Z), len(R)).
  • time_idxs (Array with same shape as Rmid) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single Rmid value at R=0.6m, Z=0.0m, t=0.26s:

R_mid_val = Eq_instance.rz2rmid(0.6, 0, 0.26)

Find R_mid values at (R, Z) points (0.6m, 0m) and (0.8m, 0m) at the single time t=0.26s. Note that the Z vector must be fully specified, even if the values are all the same:

R_mid_arr = Eq_instance.rz2rmid([0.6, 0.8], [0, 0], 0.26)

Find Rmid values at (R, Z) points (0.6m, 0m) at times t=[0.2s, 0.3s]:

R_mid_arr = Eq_instance.rz2rmid(0.6, 0, [0.2, 0.3])

Find Rmid values at (R, Z, t) points (0.6m, 0m, 0.2s) and (0.5m, 0.2m, 0.3s):

R_mid_arr = Eq_instance.rz2rmid([0.6, 0.5], [0, 0.2], [0.2, 0.3], each_t=False)

Find Rmid values on grid defined by 1D vector of radial positions R and 1D vector of vertical positions Z at time t=0.2s:

R_mid_mat = Eq_instance.rz2rmid(R, Z, 0.2, make_grid=True)
rz2roa(*args, **kwargs)[source]

Maps the given points to the normalized minor radius, r/a.

Based on the IDL version efit_rz2rmid.pro by Steve Wolfe.

Parameters:
  • R (Array-like or scalar float) – Values of the radial coordinate to map to r/a. If R and Z are both scalar values, they are used as the coordinate pair for all of the values in t. Must have the same shape as Z unless the make_grid keyword is set. If the make_grid keyword is True, R must have exactly one dimension.
  • Z (Array-like or scalar float) – Values of the vertical coordinate to map to r/a. If R and Z are both scalar values, they are used as the coordinate pair for all of the values in t. Must have the same shape as R unless the make_grid keyword is set. If the make_grid keyword is True, Z must have exactly one dimension.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of R, Z. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as R and Z (or their meshgrid if make_grid is True).
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of r/a. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in R, Z are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of R and Z or be a scalar. Default is True (evaluate ALL R, Z at EACH element in t).
  • make_grid (Boolean) – Set to True to pass R and Z through scipy.meshgrid() before evaluating. If this is set to True, R and Z must each only have a single dimension, but can have different lengths. Default is False (do not form meshgrid).
  • length_unit (String or 1) –

    Length unit that R, Z are given in. If a string is given, it must be a valid unit specifier:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ meters

    If length_unit is 1 or None, meters are assumed. The default value is 1 (use meters).

  • k (positive int) – The degree of polynomial spline interpolation to use in converting psinorm to Rmid.
  • return_t (Boolean) – Set to True to return a tuple of (rho, time_idxs), where time_idxs is the array of time indices actually used in evaluating rho with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return rho).
Returns:

roa or (roa, time_idxs)

  • roa (Array or scalar float) - The normalized minor radius. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned. If R and Z both have the same shape then roa has this shape as well, unless the make_grid keyword was True, in which case roa has shape (len(Z), len(R)).
  • time_idxs (Array with same shape as roa) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single r/a value at R=0.6m, Z=0.0m, t=0.26s:

roa_val = Eq_instance.rz2roa(0.6, 0, 0.26)

Find r/a values at (R, Z) points (0.6m, 0m) and (0.8m, 0m) at the single time t=0.26s. Note that the Z vector must be fully specified, even if the values are all the same:

roa_arr = Eq_instance.rz2roa([0.6, 0.8], [0, 0], 0.26)

Find r/a values at (R, Z) points (0.6m, 0m) at times t=[0.2s, 0.3s]:

roa_arr = Eq_instance.rz2roa(0.6, 0, [0.2, 0.3])

Find r/a values at (R, Z, t) points (0.6m, 0m, 0.2s) and (0.5m, 0.2m, 0.3s):

roa_arr = Eq_instance.rz2roa([0.6, 0.5], [0, 0.2], [0.2, 0.3], each_t=False)

Find r/a values on grid defined by 1D vector of radial positions R and 1D vector of vertical positions Z at time t=0.2s:

roa_mat = Eq_instance.rz2roa(R, Z, 0.2, make_grid=True)
rz2rho(method, *args, **kwargs)[source]

Convert the passed (R, Z, t) coordinates into one of several coordinates.

Parameters:
  • method (String) –

    Indicates which coordinates to convert to. Valid options are:

    psinorm Normalized poloidal flux
    phinorm Normalized toroidal flux
    volnorm Normalized volume
    Rmid Midplane major radius
    r/a Normalized minor radius
    q Safety factor
    F Flux function 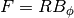F=RB_{\phi}
    FFPrime Flux function 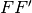FF'
    p Pressure
    pprime Pressure gradient
    v Flux surface volume

    Additionally, each valid option may be prepended with ‘sqrt’ to specify the square root of the desired unit.

  • R (Array-like or scalar float) – Values of the radial coordinate to map to rho. If R and Z are both scalar values, they are used as the coordinate pair for all of the values in t. Must have the same shape as Z unless the make_grid keyword is set. If the make_grid keyword is True, R must have exactly one dimension.
  • Z (Array-like or scalar float) – Values of the vertical coordinate to map to rho. If R and Z are both scalar values, they are used as the coordinate pair for all of the values in t. Must have the same shape as R unless the make_grid keyword is set. If the make_grid keyword is True, Z must have exactly one dimension.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of R, Z. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as R and Z (or their meshgrid if make_grid is True).
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of rho. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in R, Z are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of R and Z or be a scalar. Default is True (evaluate ALL R, Z at EACH element in t).
  • make_grid (Boolean) – Set to True to pass R and Z through scipy.meshgrid() before evaluating. If this is set to True, R and Z must each only have a single dimension, but can have different lengths. Default is False (do not form meshgrid).
  • rho (Boolean) – Set to True to return r/a (normalized minor radius) instead of Rmid when destination is Rmid. Default is False (return major radius, Rmid).
  • length_unit (String or 1) –

    Length unit that R, Z are given in, AND that Rmid is returned in. If a string is given, it must be a valid unit specifier:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ meters

    If length_unit is 1 or None, meters are assumed. The default value is 1 (use meters).

  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • return_t (Boolean) – Set to True to return a tuple of (rho, time_idxs), where time_idxs is the array of time indices actually used in evaluating rho with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return rho).
Returns:

rho or (rho, time_idxs)

  • rho (Array or scalar float) - The converted coordinates. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as rho) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.
Raises:

ValueError – If method is not one of the supported values.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single psinorm value at R=0.6m, Z=0.0m, t=0.26s:

psi_val = Eq_instance.rz2rho('psinorm', 0.6, 0, 0.26)

Find psinorm values at (R, Z) points (0.6m, 0m) and (0.8m, 0m) at the single time t=0.26s. Note that the Z vector must be fully specified, even if the values are all the same:

psi_arr = Eq_instance.rz2rho('psinorm', [0.6, 0.8], [0, 0], 0.26)

Find psinorm values at (R, Z) points (0.6m, 0m) at times t=[0.2s, 0.3s]:

psi_arr = Eq_instance.rz2rho('psinorm', 0.6, 0, [0.2, 0.3])

Find psinorm values at (R, Z, t) points (0.6m, 0m, 0.2s) and (0.5m, 0.2m, 0.3s):

psi_arr = Eq_instance.rz2rho('psinorm', [0.6, 0.5], [0, 0.2], [0.2, 0.3], each_t=False)

Find psinorm values on grid defined by 1D vector of radial positions R and 1D vector of vertical positions Z at time t=0.2s:

psi_mat = Eq_instance.rz2rho('psinorm', R, Z, 0.2, make_grid=True)
rmid2roa(R_mid, t, each_t=True, return_t=False, sqrt=False, blob=None, length_unit=1)[source]

Convert the passed (R_mid, t) coordinates into r/a.

Parameters:
  • R_mid (Array-like or scalar float) – Values of the outboard midplane major radius to map to r/a.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of R_mid. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as R_mid.
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of r/a. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in R_mid are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of R_mid or be a scalar. Default is True (evaluate ALL R_mid at EACH element in t).
  • length_unit (String or 1) –

    Length unit that R_mid is given in. If a string is given, it must be a valid unit specifier:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ meters

    If length_unit is 1 or None, meters are assumed. The default value is 1 (use meters).

  • return_t (Boolean) – Set to True to return a tuple of (rho, time_idxs), where time_idxs is the array of time indices actually used in evaluating rho with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return rho).
Returns:

roa or (roa, time_idxs)

  • roa (Array or scalar float) - Normalized midplane minor radius. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as roa) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single r/a value at R_mid=0.6m, t=0.26s:

roa_val = Eq_instance.rmid2roa(0.6, 0.26)

Find roa values at R_mid points 0.6m and 0.8m at the single time t=0.26s.:

roa_arr = Eq_instance.rmid2roa([0.6, 0.8], 0.26)

Find roa values at R_mid of 0.6m at times t=[0.2s, 0.3s]:

roa_arr = Eq_instance.rmid2roa(0.6, [0.2, 0.3])

Find r/a values at (R_mid, t) points (0.6m, 0.2s) and (0.5m, 0.3s):

roa_arr = Eq_instance.rmid2roa([0.6, 0.5], [0.2, 0.3], each_t=False)
rmid2psinorm(R_mid, t, **kwargs)[source]

Calculates the normalized poloidal flux corresponding to the passed R_mid (mapped outboard midplane major radius) values.

Parameters:
  • R_mid (Array-like or scalar float) – Values of the outboard midplane major radius to map to psinorm.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of R_mid. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as R_mid.
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of psinorm. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in R_mid are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of R_mid or be a scalar. Default is True (evaluate ALL R_mid at EACH element in t).
  • length_unit (String or 1) –

    Length unit that R_mid is given in. If a string is given, it must be a valid unit specifier:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ meters

    If length_unit is 1 or None, meters are assumed. The default value is 1 (use meters).

  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • return_t (Boolean) – Set to True to return a tuple of (rho, time_idxs), where time_idxs is the array of time indices actually used in evaluating rho with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return rho).
Returns:

psinorm or (psinorm, time_idxs)

  • psinorm (Array or scalar float) - Normalized poloidal flux. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as psinorm) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single psinorm value for Rmid=0.7m, t=0.26s:

psinorm_val = Eq_instance.rmid2psinorm(0.7, 0.26)

Find psinorm values at R_mid values of 0.5m and 0.7m at the single time t=0.26s:

psinorm_arr = Eq_instance.rmid2psinorm([0.5, 0.7], 0.26)

Find psinorm values at R_mid=0.5m at times t=[0.2s, 0.3s]:

psinorm_arr = Eq_instance.rmid2psinorm(0.5, [0.2, 0.3])

Find psinorm values at (R_mid, t) points (0.6m, 0.2s) and (0.5m, 0.3s):

psinorm_arr = Eq_instance.rmid2psinorm([0.6, 0.5], [0.2, 0.3], each_t=False)
rmid2phinorm(*args, **kwargs)[source]

Calculates the normalized toroidal flux.

Uses the definitions:

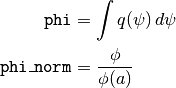
\texttt{phi} &= \int q(\psi)\,d\psi \texttt{phi\_norm} &= \frac{\phi}{\phi(a)}

This is based on the IDL version efit_rz2rho.pro by Steve Wolfe.

Parameters:
  • R_mid (Array-like or scalar float) – Values of the outboard midplane major radius to map to phinorm.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of R_mid. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as R_mid.
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of phinorm. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in R_mid are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of R_mid or be a scalar. Default is True (evaluate ALL R_mid at EACH element in t).
  • length_unit (String or 1) –

    Length unit that R_mid is given in. If a string is given, it must be a valid unit specifier:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ meters

    If length_unit is 1 or None, meters are assumed. The default value is 1 (use meters).

  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • return_t (Boolean) – Set to True to return a tuple of (rho, time_idxs), where time_idxs is the array of time indices actually used in evaluating rho with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return rho).
Returns:

phinorm or (phinorm, time_idxs)

  • phinorm (Array or scalar float) - Normalized toroidal flux. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as phinorm) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single phinorm value at R_mid=0.6m, t=0.26s:

phi_val = Eq_instance.rmid2phinorm(0.6, 0.26)

Find phinorm values at R_mid points 0.6m and 0.8m at the single time t=0.26s:

phi_arr = Eq_instance.rmid2phinorm([0.6, 0.8], 0.26)

Find phinorm values at R_mid point 0.6m at times t=[0.2s, 0.3s]:

phi_arr = Eq_instance.rmid2phinorm(0.6, [0.2, 0.3])

Find phinorm values at (R, t) points (0.6m, 0.2s) and (0.5m, 0.3s):

phi_arr = Eq_instance.rmid2phinorm([0.6, 0.5], [0.2, 0.3], each_t=False)
rmid2volnorm(*args, **kwargs)[source]

Calculates the normalized flux surface volume.

Based on the IDL version efit_rz2rho.pro by Steve Wolfe.

Parameters:
  • R_mid (Array-like or scalar float) – Values of the outboard midplane major radius to map to volnorm.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of R_mid. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as R_mid.
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of volnorm. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in R_mid are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of R_mid or be a scalar. Default is True (evaluate ALL R_mid at EACH element in t).
  • length_unit (String or 1) –

    Length unit that R_mid is given in. If a string is given, it must be a valid unit specifier:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ meters

    If length_unit is 1 or None, meters are assumed. The default value is 1 (use meters).

  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • return_t (Boolean) – Set to True to return a tuple of (rho, time_idxs), where time_idxs is the array of time indices actually used in evaluating rho with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return rho).
Returns:

volnorm or (volnorm, time_idxs)

  • volnorm (Array or scalar float) - Normalized volume. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as volnorm) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single volnorm value at R_mid=0.6m, t=0.26s:

vol_val = Eq_instance.rmid2volnorm(0.6, 0.26)

Find volnorm values at R_mid points 0.6m and 0.8m at the single time t=0.26s:

vol_arr = Eq_instance.rmid2volnorm([0.6, 0.8], 0.26)

Find volnorm values at R_mid points 0.6m at times t=[0.2s, 0.3s]:

vol_arr = Eq_instance.rmid2volnorm(0.6, [0.2, 0.3])

Find volnorm values at (R_mid, t) points (0.6m, 0.2s) and (0.5m, 0.3s):

vol_arr = Eq_instance.rmid2volnorm([0.6, 0.5], [0.2, 0.3], each_t=False)
rmid2rho(method, R_mid, t, **kwargs)[source]

Convert the passed (R_mid, t) coordinates into one of several coordinates.

Parameters:
  • method (String) –

    Indicates which coordinates to convert to. Valid options are:

    psinorm Normalized poloidal flux
    phinorm Normalized toroidal flux
    volnorm Normalized volume
    r/a Normalized minor radius
    F Flux function 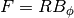F=RB_{\phi}
    FFPrime Flux function 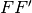FF'
    p Pressure
    pprime Pressure gradient
    v Flux surface volume

    Additionally, each valid option may be prepended with ‘sqrt’ to specify the square root of the desired unit.

  • R_mid (Array-like or scalar float) – Values of the outboard midplane major radius to map to rho.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of R_mid. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as R_mid.
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of rho. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in R_mid are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of R_mid or be a scalar. Default is True (evaluate ALL R_mid at EACH element in t).
  • length_unit (String or 1) –

    Length unit that R_mid is given in. If a string is given, it must be a valid unit specifier:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ meters

    If length_unit is 1 or None, meters are assumed. The default value is 1 (use meters).

  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • return_t (Boolean) – Set to True to return a tuple of (rho, time_idxs), where time_idxs is the array of time indices actually used in evaluating rho with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return rho).
Returns:

rho or (rho, time_idxs)

  • rho (Array or scalar float) - The converted coordinates. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as rho) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single psinorm value at R_mid=0.6m, t=0.26s:

psi_val = Eq_instance.rmid2rho('psinorm', 0.6, 0.26)

Find psinorm values at R_mid points 0.6m and 0.8m at the single time t=0.26s.:

psi_arr = Eq_instance.rmid2rho('psinorm', [0.6, 0.8], 0.26)

Find psinorm values at R_mid of 0.6m at times t=[0.2s, 0.3s]:

psi_arr = Eq_instance.rmid2rho('psinorm', 0.6, [0.2, 0.3])

Find psinorm values at (R_mid, t) points (0.6m, 0.2s) and (0.5m, 0.3s):

psi_arr = Eq_instance.rmid2rho('psinorm', [0.6, 0.5], [0.2, 0.3], each_t=False)
roa2rmid(roa, t, each_t=True, return_t=False, blob=None, length_unit=1)[source]

Convert the passed (r/a, t) coordinates into Rmid.

Parameters:
  • roa (Array-like or scalar float) – Values of the normalized minor radius to map to Rmid.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of roa. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as roa.
Keyword Arguments:
 
  • each_t (Boolean) – When True, the elements in roa are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of roa or be a scalar. Default is True (evaluate ALL roa at EACH element in t).
  • length_unit (String or 1) –

    Length unit that Rmid is returned in. If a string is given, it must be a valid unit specifier:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ meters

    If length_unit is 1 or None, meters are assumed. The default value is 1 (use meters).

  • return_t (Boolean) – Set to True to return a tuple of (rho, time_idxs), where time_idxs is the array of time indices actually used in evaluating rho with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return rho).
Returns:

Rmid or (Rmid, time_idxs)

  • Rmid (Array or scalar float) - The converted coordinates. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as Rmid) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single R_mid value at r/a=0.6, t=0.26s:

R_mid_val = Eq_instance.roa2rmid(0.6, 0.26)

Find R_mid values at r/a points 0.6 and 0.8 at the single time t=0.26s.:

R_mid_arr = Eq_instance.roa2rmid([0.6, 0.8], 0.26)

Find R_mid values at r/a of 0.6 at times t=[0.2s, 0.3s]:

R_mid_arr = Eq_instance.roa2rmid(0.6, [0.2, 0.3])

Find R_mid values at (roa, t) points (0.6, 0.2s) and (0.5, 0.3s):

R_mid_arr = Eq_instance.roa2rmid([0.6, 0.5], [0.2, 0.3], each_t=False)
roa2psinorm(*args, **kwargs)[source]

Convert the passed (r/a, t) coordinates into psinorm.

Parameters:
  • roa (Array-like or scalar float) – Values of the normalized minor radius to map to psinorm.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of roa. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as roa.
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of psinorm. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in roa are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of roa or be a scalar. Default is True (evaluate ALL roa at EACH element in t).
  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • return_t (Boolean) – Set to True to return a tuple of (rho, time_idxs), where time_idxs is the array of time indices actually used in evaluating rho with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return rho).
Returns:

psinorm or (psinorm, time_idxs)

  • psinorm (Array or scalar float) - The converted coordinates. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as psinorm) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single psinorm value at r/a=0.6, t=0.26s:

psinorm_val = Eq_instance.roa2psinorm(0.6, 0.26)

Find psinorm values at r/a points 0.6 and 0.8 at the single time t=0.26s.:

psinorm_arr = Eq_instance.roa2psinorm([0.6, 0.8], 0.26)

Find psinorm values at r/a of 0.6 at times t=[0.2s, 0.3s]:

psinorm_arr = Eq_instance.roa2psinorm(0.6, [0.2, 0.3])

Find psinorm values at (roa, t) points (0.6, 0.2s) and (0.5, 0.3s):

psinorm_arr = Eq_instance.roa2psinorm([0.6, 0.5], [0.2, 0.3], each_t=False)
roa2phinorm(*args, **kwargs)[source]

Convert the passed (r/a, t) coordinates into phinorm.

Parameters:
  • roa (Array-like or scalar float) – Values of the normalized minor radius to map to phinorm.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of roa. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as roa.
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of phinorm. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in roa are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of roa or be a scalar. Default is True (evaluate ALL roa at EACH element in t).
  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • return_t (Boolean) – Set to True to return a tuple of (rho, time_idxs), where time_idxs is the array of time indices actually used in evaluating rho with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return rho).
Returns:

phinorm or (phinorm, time_idxs)

  • phinorm (Array or scalar float) - The converted coordinates. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as phinorm) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single phinorm value at r/a=0.6, t=0.26s:

phinorm_val = Eq_instance.roa2phinorm(0.6, 0.26)

Find phinorm values at r/a points 0.6 and 0.8 at the single time t=0.26s.:

phinorm_arr = Eq_instance.roa2phinorm([0.6, 0.8], 0.26)

Find phinorm values at r/a of 0.6 at times t=[0.2s, 0.3s]:

phinorm_arr = Eq_instance.roa2phinorm(0.6, [0.2, 0.3])

Find phinorm values at (roa, t) points (0.6, 0.2s) and (0.5, 0.3s):

phinorm_arr = Eq_instance.roa2phinorm([0.6, 0.5], [0.2, 0.3], each_t=False)
roa2volnorm(*args, **kwargs)[source]

Convert the passed (r/a, t) coordinates into volnorm.

Parameters:
  • roa (Array-like or scalar float) – Values of the normalized minor radius to map to volnorm.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of roa. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as roa.
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of volnorm. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in roa are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of roa or be a scalar. Default is True (evaluate ALL roa at EACH element in t).
  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • return_t (Boolean) – Set to True to return a tuple of (rho, time_idxs), where time_idxs is the array of time indices actually used in evaluating rho with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return rho).
Returns:

volnorm or (volnorm, time_idxs)

  • volnorm (Array or scalar float) - The converted coordinates. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as volnorm) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single volnorm value at r/a=0.6, t=0.26s:

volnorm_val = Eq_instance.roa2volnorm(0.6, 0.26)

Find volnorm values at r/a points 0.6 and 0.8 at the single time t=0.26s.:

volnorm_arr = Eq_instance.roa2volnorm([0.6, 0.8], 0.26)

Find volnorm values at r/a of 0.6 at times t=[0.2s, 0.3s]:

volnorm_arr = Eq_instance.roa2volnorm(0.6, [0.2, 0.3])

Find volnorm values at (roa, t) points (0.6, 0.2s) and (0.5, 0.3s):

volnorm_arr = Eq_instance.roa2volnorm([0.6, 0.5], [0.2, 0.3], each_t=False)
roa2rho(method, *args, **kwargs)[source]

Convert the passed (r/a, t) coordinates into one of several coordinates.

Parameters:
  • method (String) –

    Indicates which coordinates to convert to. Valid options are:

    psinorm Normalized poloidal flux
    phinorm Normalized toroidal flux
    volnorm Normalized volume
    Rmid Midplane major radius
    q Safety factor
    F Flux function 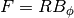F=RB_{\phi}
    FFPrime Flux function 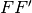FF'
    p Pressure
    pprime Pressure gradient
    v Flux surface volume

    Additionally, each valid option may be prepended with ‘sqrt’ to specify the square root of the desired unit.

  • roa (Array-like or scalar float) – Values of the normalized minor radius to map to rho.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of roa. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as roa.
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of rho. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in roa are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of roa or be a scalar. Default is True (evaluate ALL roa at EACH element in t).
  • length_unit (String or 1) –

    Length unit that Rmid is returned in. If a string is given, it must be a valid unit specifier:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ meters

    If length_unit is 1 or None, meters are assumed. The default value is 1 (use meters).

  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • return_t (Boolean) – Set to True to return a tuple of (rho, time_idxs), where time_idxs is the array of time indices actually used in evaluating rho with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return rho).
Returns:

rho or (rho, time_idxs)

  • rho (Array or scalar float) - The converted coordinates. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as rho) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single psinorm value at r/a=0.6, t=0.26s:

psi_val = Eq_instance.roa2rho('psinorm', 0.6, 0.26)

Find psinorm values at r/a points 0.6 and 0.8 at the single time t=0.26s:

psi_arr = Eq_instance.roa2rho('psinorm', [0.6, 0.8], 0.26)

Find psinorm values at r/a of 0.6 at times t=[0.2s, 0.3s]:

psi_arr = Eq_instance.roa2rho('psinorm', 0.6, [0.2, 0.3])

Find psinorm values at (r/a, t) points (0.6, 0.2s) and (0.5, 0.3s):

psi_arr = Eq_instance.roa2rho('psinorm', [0.6, 0.5], [0.2, 0.3], each_t=False)
psinorm2rmid(psi_norm, t, **kwargs)[source]

Calculates the outboard R_mid location corresponding to the passed psinorm (normalized poloidal flux) values.

Parameters:
  • psi_norm (Array-like or scalar float) – Values of the normalized poloidal flux to map to Rmid.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of psi_norm. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as psi_norm.
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of Rmid. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in psi_norm are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of psi_norm or be a scalar. Default is True (evaluate ALL psi_norm at EACH element in t).
  • rho (Boolean) – Set to True to return r/a (normalized minor radius) instead of Rmid. Default is False (return major radius, Rmid).
  • length_unit (String or 1) –

    Length unit that Rmid is returned in. If a string is given, it must be a valid unit specifier:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ meters

    If length_unit is 1 or None, meters are assumed. The default value is 1 (use meters).

  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • return_t (Boolean) – Set to True to return a tuple of (rho, time_idxs), where time_idxs is the array of time indices actually used in evaluating rho with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return rho).
Returns:

Rmid or (Rmid, time_idxs)

  • Rmid (Array or scalar float) - The converted coordinates. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as Rmid) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single R_mid value for psinorm=0.7, t=0.26s:

R_mid_val = Eq_instance.psinorm2rmid(0.7, 0.26)

Find R_mid values at psi_norm values of 0.5 and 0.7 at the single time t=0.26s:

R_mid_arr = Eq_instance.psinorm2rmid([0.5, 0.7], 0.26)

Find R_mid values at psi_norm=0.5 at times t=[0.2s, 0.3s]:

R_mid_arr = Eq_instance.psinorm2rmid(0.5, [0.2, 0.3])

Find R_mid values at (psinorm, t) points (0.6, 0.2s) and (0.5, 0.3s):

R_mid_arr = Eq_instance.psinorm2rmid([0.6, 0.5], [0.2, 0.3], each_t=False)
psinorm2roa(psi_norm, t, **kwargs)[source]

Calculates the normalized minor radius location corresponding to the passed psi_norm (normalized poloidal flux) values.

Parameters:
  • psi_norm (Array-like or scalar float) – Values of the normalized poloidal flux to map to r/a.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of psi_norm. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as psi_norm.
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of r/a. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in psi_norm are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of psi_norm or be a scalar. Default is True (evaluate ALL psi_norm at EACH element in t).
  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • return_t (Boolean) – Set to True to return a tuple of (rho, time_idxs), where time_idxs is the array of time indices actually used in evaluating rho with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return rho).
Returns:

roa or (roa, time_idxs)

  • roa (Array or scalar float) - Normalized midplane minor radius. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as roa) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single r/a value for psinorm=0.7, t=0.26s:

roa_val = Eq_instance.psinorm2roa(0.7, 0.26)

Find r/a values at psi_norm values of 0.5 and 0.7 at the single time t=0.26s:

roa_arr = Eq_instance.psinorm2roa([0.5, 0.7], 0.26)

Find r/a values at psi_norm=0.5 at times t=[0.2s, 0.3s]:

roa_arr = Eq_instance.psinorm2roa(0.5, [0.2, 0.3])

Find r/a values at (psinorm, t) points (0.6, 0.2s) and (0.5, 0.3s):

roa_arr = Eq_instance.psinorm2roa([0.6, 0.5], [0.2, 0.3], each_t=False)
psinorm2volnorm(psi_norm, t, **kwargs)[source]

Calculates the normalized volume corresponding to the passed psi_norm (normalized poloidal flux) values.

Parameters:
  • psi_norm (Array-like or scalar float) – Values of the normalized poloidal flux to map to volnorm.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of psi_norm. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as psi_norm.
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of volnorm. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in psi_norm are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of psi_norm or be a scalar. Default is True (evaluate ALL psi_norm at EACH element in t).
  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • return_t (Boolean) – Set to True to return a tuple of (rho, time_idxs), where time_idxs is the array of time indices actually used in evaluating rho with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return rho).
Returns:

volnorm or (volnorm, time_idxs)

  • volnorm (Array or scalar float) - The converted coordinates. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as volnorm) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single volnorm value for psinorm=0.7, t=0.26s:

volnorm_val = Eq_instance.psinorm2volnorm(0.7, 0.26)

Find volnorm values at psi_norm values of 0.5 and 0.7 at the single time t=0.26s:

volnorm_arr = Eq_instance.psinorm2volnorm([0.5, 0.7], 0.26)

Find volnorm values at psi_norm=0.5 at times t=[0.2s, 0.3s]:

volnorm_arr = Eq_instance.psinorm2volnorm(0.5, [0.2, 0.3])

Find volnorm values at (psinorm, t) points (0.6, 0.2s) and (0.5, 0.3s):

volnorm_arr = Eq_instance.psinorm2volnorm([0.6, 0.5], [0.2, 0.3], each_t=False)
psinorm2phinorm(psi_norm, t, **kwargs)[source]

Calculates the normalized toroidal flux corresponding to the passed psi_norm (normalized poloidal flux) values.

Parameters:
  • psi_norm (Array-like or scalar float) – Values of the normalized poloidal flux to map to phinorm.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of psi_norm. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as psi_norm.
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of phinorm. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in psi_norm are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of psi_norm or be a scalar. Default is True (evaluate ALL psi_norm at EACH element in t).
  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • return_t (Boolean) – Set to True to return a tuple of (rho, time_idxs), where time_idxs is the array of time indices actually used in evaluating rho with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return rho).
Returns:

phinorm or (phinorm, time_idxs)

  • phinorm (Array or scalar float) - The converted coordinates. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as phinorm) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single phinorm value for psinorm=0.7, t=0.26s:

phinorm_val = Eq_instance.psinorm2phinorm(0.7, 0.26)

Find phinorm values at psi_norm values of 0.5 and 0.7 at the single time t=0.26s:

phinorm_arr = Eq_instance.psinorm2phinorm([0.5, 0.7], 0.26)

Find phinorm values at psi_norm=0.5 at times t=[0.2s, 0.3s]:

phinorm_arr = Eq_instance.psinorm2phinorm(0.5, [0.2, 0.3])

Find phinorm values at (psinorm, t) points (0.6, 0.2s) and (0.5, 0.3s):

phinorm_arr = Eq_instance.psinorm2phinorm([0.6, 0.5], [0.2, 0.3], each_t=False)
psinorm2rho(method, *args, **kwargs)[source]

Convert the passed (psinorm, t) coordinates into one of several coordinates.

Parameters:
  • method (String) –

    Indicates which coordinates to convert to. Valid options are:

    phinorm Normalized toroidal flux
    volnorm Normalized volume
    Rmid Midplane major radius
    r/a Normalized minor radius
    q Safety factor
    F Flux function 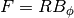F=RB_{\phi}
    FFPrime Flux function 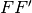FF'
    p Pressure
    pprime Pressure gradient
    v Flux surface volume

    Additionally, each valid option may be prepended with ‘sqrt’ to specify the square root of the desired unit.

  • psi_norm (Array-like or scalar float) – Values of the normalized poloidal flux to map to rho.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of psi_norm. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as psi_norm.
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of rho. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in psi_norm are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of psi_norm or be a scalar. Default is True (evaluate ALL psi_norm at EACH element in t).
  • rho (Boolean) – Set to True to return r/a (normalized minor radius) instead of Rmid. Default is False (return major radius, Rmid).
  • length_unit (String or 1) –

    Length unit that Rmid is returned in. If a string is given, it must be a valid unit specifier:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ meters

    If length_unit is 1 or None, meters are assumed. The default value is 1 (use meters).

  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • return_t (Boolean) – Set to True to return a tuple of (rho, time_idxs), where time_idxs is the array of time indices actually used in evaluating rho with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return rho).
Returns:

rho or (rho, time_idxs)

  • rho (Array or scalar float) - The converted coordinates. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as rho) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.
Raises:

ValueError – If method is not one of the supported values.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single phinorm value at psinorm=0.6, t=0.26s:

phi_val = Eq_instance.psinorm2rho('phinorm', 0.6, 0.26)

Find phinorm values at phinorm of 0.6 and 0.8 at the single time t=0.26s:

phi_arr = Eq_instance.psinorm2rho('phinorm', [0.6, 0.8], 0.26)

Find phinorm values at psinorm of 0.6 at times t=[0.2s, 0.3s]:

phi_arr = Eq_instance.psinorm2rho('phinorm', 0.6, [0.2, 0.3])

Find phinorm values at (psinorm, t) points (0.6, 0.2s) and (0.5m, 0.3s):

phi_arr = Eq_instance.psinorm2rho('phinorm', [0.6, 0.5], [0.2, 0.3], each_t=False)
phinorm2psinorm(phinorm, t, **kwargs)[source]

Calculates the normalized poloidal flux corresponding to the passed phinorm (normalized toroidal flux) values.

Parameters:
  • phinorm (Array-like or scalar float) – Values of the normalized toroidal flux to map to psinorm.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of phinorm. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as phinorm.
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of psinorm. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in phinorm are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of phinorm or be a scalar. Default is True (evaluate ALL phinorm at EACH element in t).
  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • return_t (Boolean) – Set to True to return a tuple of (rho, time_idxs), where time_idxs is the array of time indices actually used in evaluating rho with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return rho).
Returns:

psinorm or (psinorm, time_idxs)

  • psinorm (Array or scalar float) - The converted coordinates. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as psinorm) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single psinorm value for phinorm=0.7, t=0.26s:

psinorm_val = Eq_instance.phinorm2psinorm(0.7, 0.26)

Find psinorm values at phinorm values of 0.5 and 0.7 at the single time t=0.26s:

psinorm_arr = Eq_instance.phinorm2psinorm([0.5, 0.7], 0.26)

Find psinorm values at phinorm=0.5 at times t=[0.2s, 0.3s]:

psinorm_arr = Eq_instance.phinorm2psinorm(0.5, [0.2, 0.3])

Find psinorm values at (phinorm, t) points (0.6, 0.2s) and (0.5, 0.3s):

psinorm_arr = Eq_instance.phinorm2psinorm([0.6, 0.5], [0.2, 0.3], each_t=False)
phinorm2volnorm(*args, **kwargs)[source]

Calculates the normalized flux surface volume corresponding to the passed phinorm (normalized toroidal flux) values.

Parameters:
  • phinorm (Array-like or scalar float) – Values of the normalized toroidal flux to map to volnorm.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of phinorm. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as phinorm.
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of volnorm. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in phinorm are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of phinorm or be a scalar. Default is True (evaluate ALL phinorm at EACH element in t).
  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • return_t (Boolean) – Set to True to return a tuple of (rho, time_idxs), where time_idxs is the array of time indices actually used in evaluating rho with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return rho).
Returns:

volnorm or (volnorm, time_idxs)

  • volnorm (Array or scalar float) - The converted coordinates. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as volnorm) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single volnorm value for phinorm=0.7, t=0.26s:

volnorm_val = Eq_instance.phinorm2volnorm(0.7, 0.26)

Find volnorm values at phinorm values of 0.5 and 0.7 at the single time t=0.26s:

volnorm_arr = Eq_instance.phinorm2volnorm([0.5, 0.7], 0.26)

Find volnorm values at phinorm=0.5 at times t=[0.2s, 0.3s]:

volnorm_arr = Eq_instance.phinorm2volnorm(0.5, [0.2, 0.3])

Find volnorm values at (phinorm, t) points (0.6, 0.2s) and (0.5, 0.3s):

volnorm_arr = Eq_instance.phinorm2volnorm([0.6, 0.5], [0.2, 0.3], each_t=False)
phinorm2rmid(*args, **kwargs)[source]

Calculates the mapped outboard midplane major radius corresponding to the passed phinorm (normalized toroidal flux) values.

Parameters:
  • phinorm (Array-like or scalar float) – Values of the normalized toroidal flux to map to Rmid.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of phinorm. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as phinorm.
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of Rmid. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in phinorm are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of phinorm or be a scalar. Default is True (evaluate ALL phinorm at EACH element in t).
  • rho (Boolean) – Set to True to return r/a (normalized minor radius) instead of Rmid. Default is False (return major radius, Rmid).
  • length_unit (String or 1) –

    Length unit that Rmid is returned in. If a string is given, it must be a valid unit specifier:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ meters

    If length_unit is 1 or None, meters are assumed. The default value is 1 (use meters).

  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • return_t (Boolean) – Set to True to return a tuple of (rho, time_idxs), where time_idxs is the array of time indices actually used in evaluating rho with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return rho).
Returns:

Rmid or (Rmid, time_idxs)

  • Rmid (Array or scalar float) - The converted coordinates. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as Rmid) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single Rmid value for phinorm=0.7, t=0.26s:

Rmid_val = Eq_instance.phinorm2rmid(0.7, 0.26)

Find Rmid values at phinorm values of 0.5 and 0.7 at the single time t=0.26s:

Rmid_arr = Eq_instance.phinorm2rmid([0.5, 0.7], 0.26)

Find Rmid values at phinorm=0.5 at times t=[0.2s, 0.3s]:

Rmid_arr = Eq_instance.phinorm2rmid(0.5, [0.2, 0.3])

Find Rmid values at (phinorm, t) points (0.6, 0.2s) and (0.5, 0.3s):

Rmid_arr = Eq_instance.phinorm2rmid([0.6, 0.5], [0.2, 0.3], each_t=False)
phinorm2roa(phi_norm, t, **kwargs)[source]

Calculates the normalized minor radius corresponding to the passed phinorm (normalized toroidal flux) values.

Parameters:
  • phinorm (Array-like or scalar float) – Values of the normalized toroidal flux to map to r/a.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of phinorm. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as phinorm.
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of r/a. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in phinorm are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of phinorm or be a scalar. Default is True (evaluate ALL phinorm at EACH element in t).
  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • return_t (Boolean) – Set to True to return a tuple of (rho, time_idxs), where time_idxs is the array of time indices actually used in evaluating rho with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return rho).
Returns:

roa or (roa, time_idxs)

  • roa (Array or scalar float) - Normalized midplane minor radius. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as roa) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single r/a value for phinorm=0.7, t=0.26s:

roa_val = Eq_instance.phinorm2roa(0.7, 0.26)

Find r/a values at phinorm values of 0.5 and 0.7 at the single time t=0.26s:

roa_arr = Eq_instance.phinorm2roa([0.5, 0.7], 0.26)

Find r/a values at phinorm=0.5 at times t=[0.2s, 0.3s]:

roa_arr = Eq_instance.phinorm2roa(0.5, [0.2, 0.3])

Find r/a values at (phinorm, t) points (0.6, 0.2s) and (0.5, 0.3s):

roa_arr = Eq_instance.phinorm2roa([0.6, 0.5], [0.2, 0.3], each_t=False)
phinorm2rho(method, *args, **kwargs)[source]

Convert the passed (phinorm, t) coordinates into one of several coordinates.

Parameters:
  • method (String) –

    Indicates which coordinates to convert to. Valid options are:

    psinorm Normalized poloidal flux
    volnorm Normalized volume
    Rmid Midplane major radius
    r/a Normalized minor radius
    q Safety factor
    F Flux function 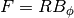F=RB_{\phi}
    FFPrime Flux function 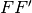FF'
    p Pressure
    pprime Pressure gradient
    v Flux surface volume

    Additionally, each valid option may be prepended with ‘sqrt’ to specify the square root of the desired unit.

  • phinorm (Array-like or scalar float) – Values of the normalized toroidal flux to map to rho.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of phinorm. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as phinorm.
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of rho. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in phinorm are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of phinorm or be a scalar. Default is True (evaluate ALL phinorm at EACH element in t).
  • rho (Boolean) – Set to True to return r/a (normalized minor radius) instead of Rmid. Default is False (return major radius, Rmid).
  • length_unit (String or 1) –

    Length unit that Rmid is returned in. If a string is given, it must be a valid unit specifier:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ meters

    If length_unit is 1 or None, meters are assumed. The default value is 1 (use meters).

  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • return_t (Boolean) – Set to True to return a tuple of (rho, time_idxs), where time_idxs is the array of time indices actually used in evaluating rho with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return rho).
Returns:

rho or (rho, time_idxs)

  • rho (Array or scalar float) - The converted coordinates. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as rho) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.
Raises:

ValueError – If method is not one of the supported values.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single psinorm value at phinorm=0.6, t=0.26s:

psi_val = Eq_instance.phinorm2rho('psinorm', 0.6, 0.26)

Find psinorm values at phinorm of 0.6 and 0.8 at the single time t=0.26s:

psi_arr = Eq_instance.phinorm2rho('psinorm', [0.6, 0.8], 0.26)

Find psinorm values at phinorm of 0.6 at times t=[0.2s, 0.3s]:

psi_arr = Eq_instance.phinorm2rho('psinorm', 0.6, [0.2, 0.3])

Find psinorm values at (phinorm, t) points (0.6, 0.2s) and (0.5m, 0.3s):

psi_arr = Eq_instance.phinorm2rho('psinorm', [0.6, 0.5], [0.2, 0.3], each_t=False)
volnorm2psinorm(*args, **kwargs)[source]

Calculates the normalized poloidal flux corresponding to the passed volnorm (normalized flux surface volume) values.

Parameters:
  • volnorm (Array-like or scalar float) – Values of the normalized flux surface volume to map to psinorm.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of volnorm. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as volnorm.
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of psinorm. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in volnorm are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of volnorm or be a scalar. Default is True (evaluate ALL volnorm at EACH element in t).
  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • return_t (Boolean) – Set to True to return a tuple of (rho, time_idxs), where time_idxs is the array of time indices actually used in evaluating rho with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return rho).
Returns:

psinorm or (psinorm, time_idxs)

  • psinorm (Array or scalar float) - The converted coordinates. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as psinorm) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single psinorm value for volnorm=0.7, t=0.26s:

psinorm_val = Eq_instance.volnorm2psinorm(0.7, 0.26)

Find psinorm values at volnorm values of 0.5 and 0.7 at the single time t=0.26s:

psinorm_arr = Eq_instance.volnorm2psinorm([0.5, 0.7], 0.26)

Find psinorm values at volnorm=0.5 at times t=[0.2s, 0.3s]:

psinorm_arr = Eq_instance.volnorm2psinorm(0.5, [0.2, 0.3])

Find psinorm values at (volnorm, t) points (0.6, 0.2s) and (0.5, 0.3s):

psinorm_arr = Eq_instance.volnorm2psinorm([0.6, 0.5], [0.2, 0.3], each_t=False)
volnorm2phinorm(*args, **kwargs)[source]

Calculates the normalized toroidal flux corresponding to the passed volnorm (normalized flux surface volume) values.

Parameters:
  • volnorm (Array-like or scalar float) – Values of the normalized flux surface volume to map to phinorm.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of volnorm. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as volnorm.
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of phinorm. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in volnorm are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of volnorm or be a scalar. Default is True (evaluate ALL volnorm at EACH element in t).
  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • return_t (Boolean) – Set to True to return a tuple of (rho, time_idxs), where time_idxs is the array of time indices actually used in evaluating rho with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return rho).
Returns:

phinorm or (phinorm, time_idxs)

  • phinorm (Array or scalar float) - The converted coordinates. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as phinorm) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single phinorm value for volnorm=0.7, t=0.26s:

phinorm_val = Eq_instance.volnorm2phinorm(0.7, 0.26)

Find phinorm values at volnorm values of 0.5 and 0.7 at the single time t=0.26s:

phinorm_arr = Eq_instance.volnorm2phinorm([0.5, 0.7], 0.26)

Find phinorm values at volnorm=0.5 at times t=[0.2s, 0.3s]:

phinorm_arr = Eq_instance.volnorm2phinorm(0.5, [0.2, 0.3])

Find phinorm values at (volnorm, t) points (0.6, 0.2s) and (0.5, 0.3s):

phinorm_arr = Eq_instance.volnorm2phinorm([0.6, 0.5], [0.2, 0.3], each_t=False)
volnorm2rmid(*args, **kwargs)[source]

Calculates the mapped outboard midplane major radius corresponding to the passed volnorm (normalized flux surface volume) values.

Parameters:
  • volnorm (Array-like or scalar float) – Values of the normalized flux surface volume to map to Rmid.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of volnorm. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as volnorm.
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of Rmid. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in volnorm are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of volnorm or be a scalar. Default is True (evaluate ALL volnorm at EACH element in t).
  • rho (Boolean) – Set to True to return r/a (normalized minor radius) instead of Rmid. Default is False (return major radius, Rmid).
  • length_unit (String or 1) –

    Length unit that Rmid is returned in. If a string is given, it must be a valid unit specifier:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ meters

    If length_unit is 1 or None, meters are assumed. The default value is 1 (use meters).

  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • return_t (Boolean) – Set to True to return a tuple of (rho, time_idxs), where time_idxs is the array of time indices actually used in evaluating rho with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return rho).
Returns:

Rmid or (Rmid, time_idxs)

  • Rmid (Array or scalar float) - The converted coordinates. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as Rmid) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single Rmid value for volnorm=0.7, t=0.26s:

Rmid_val = Eq_instance.volnorm2rmid(0.7, 0.26)

Find Rmid values at volnorm values of 0.5 and 0.7 at the single time t=0.26s:

Rmid_arr = Eq_instance.volnorm2rmid([0.5, 0.7], 0.26)

Find Rmid values at volnorm=0.5 at times t=[0.2s, 0.3s]:

Rmid_arr = Eq_instance.volnorm2rmid(0.5, [0.2, 0.3])

Find Rmid values at (volnorm, t) points (0.6, 0.2s) and (0.5, 0.3s):

Rmid_arr = Eq_instance.volnorm2rmid([0.6, 0.5], [0.2, 0.3], each_t=False)
volnorm2roa(*args, **kwargs)[source]

Calculates the normalized minor radius corresponding to the passed volnorm (normalized flux surface volume) values.

Parameters:
  • volnorm (Array-like or scalar float) – Values of the normalized flux surface volume to map to r/a.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of volnorm. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as volnorm.
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of r/a. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in volnorm are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of volnorm or be a scalar. Default is True (evaluate ALL volnorm at EACH element in t).
  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • return_t (Boolean) – Set to True to return a tuple of (rho, time_idxs), where time_idxs is the array of time indices actually used in evaluating rho with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return rho).
Returns:

roa or (roa, time_idxs)

  • roa (Array or scalar float) - The converted coordinates. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as roa) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single r/a value for volnorm=0.7, t=0.26s:

roa_val = Eq_instance.volnorm2roa(0.7, 0.26)

Find r/a values at volnorm values of 0.5 and 0.7 at the single time t=0.26s:

roa_arr = Eq_instance.volnorm2roa([0.5, 0.7], 0.26)

Find r/a values at volnorm=0.5 at times t=[0.2s, 0.3s]:

roa_arr = Eq_instance.volnorm2roa(0.5, [0.2, 0.3])

Find r/a values at (volnorm, t) points (0.6, 0.2s) and (0.5, 0.3s):

roa_arr = Eq_instance.volnorm2roa([0.6, 0.5], [0.2, 0.3], each_t=False)
volnorm2rho(method, *args, **kwargs)[source]

Convert the passed (volnorm, t) coordinates into one of several coordinates.

Parameters:
  • method (String) –

    Indicates which coordinates to convert to. Valid options are:

    psinorm Normalized poloidal flux
    phinorm Normalized toroidal flux
    Rmid Midplane major radius
    r/a Normalized minor radius
    q Safety factor
    F Flux function 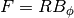F=RB_{\phi}
    FFPrime Flux function 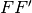FF'
    p Pressure
    pprime Pressure gradient
    v Flux surface volume

    Additionally, each valid option may be prepended with ‘sqrt’ to specify the square root of the desired unit.

  • volnorm (Array-like or scalar float) – Values of the normalized flux surface volume to map to rho.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of volnorm. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as volnorm.
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of rho. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in volnorm are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of volnorm or be a scalar. Default is True (evaluate ALL volnorm at EACH element in t).
  • rho (Boolean) – Set to True to return r/a (normalized minor radius) instead of Rmid. Default is False (return major radius, Rmid).
  • length_unit (String or 1) –

    Length unit that Rmid is returned in. If a string is given, it must be a valid unit specifier:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ meters

    If length_unit is 1 or None, meters are assumed. The default value is 1 (use meters).

  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • return_t (Boolean) – Set to True to return a tuple of (rho, time_idxs), where time_idxs is the array of time indices actually used in evaluating rho with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return rho).
Returns:

rho or (rho, time_idxs)

  • rho (Array or scalar float) - The converted coordinates. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as rho) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.
Raises:

ValueError – If method is not one of the supported values.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single psinorm value at volnorm=0.6, t=0.26s:

psi_val = Eq_instance.volnorm2rho('psinorm', 0.6, 0.26)

Find psinorm values at volnorm of 0.6 and 0.8 at the single time t=0.26s:

psi_arr = Eq_instance.volnorm2rho('psinorm', [0.6, 0.8], 0.26)

Find psinorm values at volnorm of 0.6 at times t=[0.2s, 0.3s]:

psi_arr = Eq_instance.volnorm2rho('psinorm', 0.6, [0.2, 0.3])

Find psinorm values at (volnorm, t) points (0.6, 0.2s) and (0.5m, 0.3s):

psi_arr = Eq_instance.volnorm2rho('psinorm', [0.6, 0.5], [0.2, 0.3], each_t=False)
rz2q(R, Z, t, **kwargs)[source]

Calculates the safety factor (“q”) at the given (R, Z, t).

By default, EFIT only computes this inside the LCFS.

Parameters:
  • R (Array-like or scalar float) – Values of the radial coordinate to map to q. If R and Z are both scalar values, they are used as the coordinate pair for all of the values in t. Must have the same shape as Z unless the make_grid keyword is set. If the make_grid keyword is True, R must have exactly one dimension.
  • Z (Array-like or scalar float) – Values of the vertical coordinate to map to q. If R and Z are both scalar values, they are used as the coordinate pair for all of the values in t. Must have the same shape as R unless the make_grid keyword is set. If the make_grid keyword is True, Z must have exactly one dimension.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of R, Z. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as R and Z (or their meshgrid if make_grid is True).
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of q. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in R, Z are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of R and Z or be a scalar. Default is True (evaluate ALL R, Z at EACH element in t).
  • make_grid (Boolean) – Set to True to pass R and Z through scipy.meshgrid() before evaluating. If this is set to True, R and Z must each only have a single dimension, but can have different lengths. Default is False (do not form meshgrid).
  • length_unit (String or 1) –

    Length unit that R, Z are given in. If a string is given, it must be a valid unit specifier:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ meters

    If length_unit is 1 or None, meters are assumed. The default value is 1 (use meters).

  • return_t (Boolean) – Set to True to return a tuple of (q, time_idxs), where time_idxs is the array of time indices actually used in evaluating q with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return q).
Returns:

q or (q, time_idxs)

  • q (Array or scalar float) - The safety factor (“q”). If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned. If R and Z both have the same shape then q has this shape as well, unless the make_grid keyword was True, in which case q has shape (len(Z), len(R)).
  • time_idxs (Array with same shape as q) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single q value at R=0.6m, Z=0.0m, t=0.26s:

q_val = Eq_instance.rz2q(0.6, 0, 0.26)

Find q values at (R, Z) points (0.6m, 0m) and (0.8m, 0m) at the single time t=0.26s. Note that the Z vector must be fully specified, even if the values are all the same:

q_arr = Eq_instance.rz2q([0.6, 0.8], [0, 0], 0.26)

Find q values at (R, Z) points (0.6m, 0m) at times t=[0.2s, 0.3s]:

q_arr = Eq_instance.rz2q(0.6, 0, [0.2, 0.3])

Find q values at (R, Z, t) points (0.6m, 0m, 0.2s) and (0.5m, 0.2m, 0.3s):

q_arr = Eq_instance.rz2q([0.6, 0.5], [0, 0.2], [0.2, 0.3], each_t=False)

Find q values on grid defined by 1D vector of radial positions R and 1D vector of vertical positions Z at time t=0.2s:

q_mat = Eq_instance.rz2q(R, Z, 0.2, make_grid=True)
rmid2q(R_mid, t, **kwargs)[source]

Calculates the safety factor (“q”) corresponding to the passed R_mid (mapped outboard midplane major radius) values.

By default, EFIT only computes this inside the LCFS.

Parameters:
  • R_mid (Array-like or scalar float) – Values of the outboard midplane major radius to map to q.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of R_mid. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as R_mid.
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of q. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in R_mid are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of R_mid or be a scalar. Default is True (evaluate ALL R_mid at EACH element in t).
  • length_unit (String or 1) –

    Length unit that R_mid is given in. If a string is given, it must be a valid unit specifier:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ meters

    If length_unit is 1 or None, meters are assumed. The default value is 1 (use meters).

  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • return_t (Boolean) – Set to True to return a tuple of (q, time_idxs), where time_idxs is the array of time indices actually used in evaluating q with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return q).
Returns:

q or (q, time_idxs)

  • q (Array or scalar float) - The safety factor (“q”). If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as q) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single q value for Rmid=0.7m, t=0.26s:

q_val = Eq_instance.rmid2q(0.7, 0.26)

Find q values at R_mid values of 0.5m and 0.7m at the single time t=0.26s:

q_arr = Eq_instance.rmid2q([0.5, 0.7], 0.26)

Find q values at R_mid=0.5m at times t=[0.2s, 0.3s]:

q_arr = Eq_instance.rmid2q(0.5, [0.2, 0.3])

Find q values at (R_mid, t) points (0.6m, 0.2s) and (0.5m, 0.3s):

q_arr = Eq_instance.rmid2q([0.6, 0.5], [0.2, 0.3], each_t=False)
roa2q(roa, t, **kwargs)[source]

Convert the passed (r/a, t) coordinates into safety factor (“q”).

By default, EFIT only computes this inside the LCFS.

Parameters:
  • roa (Array-like or scalar float) – Values of the normalized minor radius to map to q.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of roa. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as roa.
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of q. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in roa are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of roa or be a scalar. Default is True (evaluate ALL roa at EACH element in t).
  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • return_t (Boolean) – Set to True to return a tuple of (q, time_idxs), where time_idxs is the array of time indices actually used in evaluating q with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return q).
Returns:

q or (q, time_idxs)

  • q (Array or scalar float) - The safety factor (“q”). If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as q) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single q value at r/a=0.6, t=0.26s:

q_val = Eq_instance.roa2q(0.6, 0.26)

Find q values at r/a points 0.6 and 0.8 at the single time t=0.26s.:

q_arr = Eq_instance.roa2q([0.6, 0.8], 0.26)

Find q values at r/a of 0.6 at times t=[0.2s, 0.3s]:

q_arr = Eq_instance.roa2q(0.6, [0.2, 0.3])

Find q values at (roa, t) points (0.6, 0.2s) and (0.5, 0.3s):

q_arr = Eq_instance.roa2q([0.6, 0.5], [0.2, 0.3], each_t=False)
psinorm2q(psinorm, t, **kwargs)[source]

Calculates the safety factor (“q”) corresponding to the passed psi_norm (normalized poloidal flux) values.

By default, EFIT only computes this inside the LCFS.

Parameters:
  • psi_norm (Array-like or scalar float) – Values of the normalized poloidal flux to map to q.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of psi_norm. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as psi_norm.
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of q. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in psi_norm are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of psi_norm or be a scalar. Default is True (evaluate ALL psi_norm at EACH element in t).
  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • return_t (Boolean) – Set to True to return a tuple of (q, time_idxs), where time_idxs is the array of time indices actually used in evaluating q with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return q).
Returns:

q or (q, time_idxs)

  • q (Array or scalar float) - The safety factor (“q”). If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as q) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single q value for psinorm=0.7, t=0.26s:

q_val = Eq_instance.psinorm2q(0.7, 0.26)

Find q values at psi_norm values of 0.5 and 0.7 at the single time t=0.26s:

q_arr = Eq_instance.psinorm2q([0.5, 0.7], 0.26)

Find q values at psi_norm=0.5 at times t=[0.2s, 0.3s]:

q_arr = Eq_instance.psinorm2q(0.5, [0.2, 0.3])

Find q values at (psinorm, t) points (0.6, 0.2s) and (0.5, 0.3s):

q_arr = Eq_instance.psinorm2q([0.6, 0.5], [0.2, 0.3], each_t=False)
phinorm2q(phinorm, t, **kwargs)[source]

Calculates the safety factor (“q”) corresponding to the passed phinorm (normalized toroidal flux) values.

By default, EFIT only computes this inside the LCFS.

Parameters:
  • phinorm (Array-like or scalar float) – Values of the normalized toroidal flux to map to q.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of phinorm. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as phinorm.
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of q. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in phinorm are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of phinorm or be a scalar. Default is True (evaluate ALL phinorm at EACH element in t).
  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • return_t (Boolean) – Set to True to return a tuple of (q, time_idxs), where time_idxs is the array of time indices actually used in evaluating q with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return q).
Returns:

q or (q, time_idxs)

  • q (Array or scalar float) - The safety factor (“q”). If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as q) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single q value for phinorm=0.7, t=0.26s:

q_val = Eq_instance.phinorm2q(0.7, 0.26)

Find q values at phinorm values of 0.5 and 0.7 at the single time t=0.26s:

q_arr = Eq_instance.phinorm2q([0.5, 0.7], 0.26)

Find q values at phinorm=0.5 at times t=[0.2s, 0.3s]:

q_arr = Eq_instance.phinorm2q(0.5, [0.2, 0.3])

Find q values at (phinorm, t) points (0.6, 0.2s) and (0.5, 0.3s):

q_arr = Eq_instance.phinorm2q([0.6, 0.5], [0.2, 0.3], each_t=False)
volnorm2q(volnorm, t, **kwargs)[source]

Calculates the safety factor (“q”) corresponding to the passed volnorm (normalized flux surface volume) values.

By default, EFIT only computes this inside the LCFS.

Parameters:
  • volnorm (Array-like or scalar float) – Values of the normalized flux surface volume to map to q.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of volnorm. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as volnorm.
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of q. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in volnorm are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of volnorm or be a scalar. Default is True (evaluate ALL volnorm at EACH element in t).
  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • return_t (Boolean) – Set to True to return a tuple of (q, time_idxs), where time_idxs is the array of time indices actually used in evaluating q with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return q).
Returns:

q or (q, time_idxs)

  • q (Array or scalar float) - The safety factor (“q”). If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as q) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single q value for volnorm=0.7, t=0.26s:

q_val = Eq_instance.volnorm2q(0.7, 0.26)

Find q values at volnorm values of 0.5 and 0.7 at the single time t=0.26s:

q_arr = Eq_instance.volnorm2q([0.5, 0.7], 0.26)

Find q values at volnorm=0.5 at times t=[0.2s, 0.3s]:

q_arr = Eq_instance.volnorm2q(0.5, [0.2, 0.3])

Find q values at (volnorm, t) points (0.6, 0.2s) and (0.5, 0.3s):

q_arr = Eq_instance.volnorm2q([0.6, 0.5], [0.2, 0.3], each_t=False)
rz2F(R, Z, t, **kwargs)[source]

Calculates the flux function 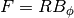F=RB_{\phi} at the given (R, Z, t).

By default, EFIT only computes this inside the LCFS.

Parameters:
  • R (Array-like or scalar float) – Values of the radial coordinate to map to F. If R and Z are both scalar values, they are used as the coordinate pair for all of the values in t. Must have the same shape as Z unless the make_grid keyword is set. If the make_grid keyword is True, R must have exactly one dimension.
  • Z (Array-like or scalar float) – Values of the vertical coordinate to map to F. If R and Z are both scalar values, they are used as the coordinate pair for all of the values in t. Must have the same shape as R unless the make_grid keyword is set. If the make_grid keyword is True, Z must have exactly one dimension.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of R, Z. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as R and Z (or their meshgrid if make_grid is True).
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of F. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in R, Z are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of R and Z or be a scalar. Default is True (evaluate ALL R, Z at EACH element in t).
  • make_grid (Boolean) – Set to True to pass R and Z through scipy.meshgrid() before evaluating. If this is set to True, R and Z must each only have a single dimension, but can have different lengths. Default is False (do not form meshgrid).
  • length_unit (String or 1) –

    Length unit that R, Z are given in. If a string is given, it must be a valid unit specifier:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ meters

    If length_unit is 1 or None, meters are assumed. The default value is 1 (use meters).

  • return_t (Boolean) – Set to True to return a tuple of (F, time_idxs), where time_idxs is the array of time indices actually used in evaluating F with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return F).
Returns:

F or (F, time_idxs)

  • F (Array or scalar float) - The flux function 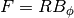F=RB_{\phi}. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned. If R and Z both have the same shape then F has this shape as well, unless the make_grid keyword was True, in which case F has shape (len(Z), len(R)).
  • time_idxs (Array with same shape as F) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single F value at R=0.6m, Z=0.0m, t=0.26s:

F_val = Eq_instance.rz2F(0.6, 0, 0.26)

Find F values at (R, Z) points (0.6m, 0m) and (0.8m, 0m) at the single time t=0.26s. Note that the Z vector must be fully specified, even if the values are all the same:

F_arr = Eq_instance.rz2F([0.6, 0.8], [0, 0], 0.26)

Find F values at (R, Z) points (0.6m, 0m) at times t=[0.2s, 0.3s]:

F_arr = Eq_instance.rz2F(0.6, 0, [0.2, 0.3])

Find F values at (R, Z, t) points (0.6m, 0m, 0.2s) and (0.5m, 0.2m, 0.3s):

F_arr = Eq_instance.rz2F([0.6, 0.5], [0, 0.2], [0.2, 0.3], each_t=False)

Find F values on grid defined by 1D vector of radial positions R and 1D vector of vertical positions Z at time t=0.2s:

F_mat = Eq_instance.rz2F(R, Z, 0.2, make_grid=True)
rmid2F(R_mid, t, **kwargs)[source]

Calculates the flux function 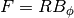F=RB_{\phi} corresponding to the passed R_mid (mapped outboard midplane major radius) values.

By default, EFIT only computes this inside the LCFS.

Parameters:
  • R_mid (Array-like or scalar float) – Values of the outboard midplane major radius to map to F.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of R_mid. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as R_mid.
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of F. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in R_mid are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of R_mid or be a scalar. Default is True (evaluate ALL R_mid at EACH element in t).
  • length_unit (String or 1) –

    Length unit that R_mid is given in. If a string is given, it must be a valid unit specifier:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ meters

    If length_unit is 1 or None, meters are assumed. The default value is 1 (use meters).

  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • return_t (Boolean) – Set to True to return a tuple of (F, time_idxs), where time_idxs is the array of time indices actually used in evaluating F with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return F).
Returns:

F or (F, time_idxs)

  • F (Array or scalar float) - The flux function 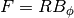F=RB_{\phi}. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as F) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single F value for Rmid=0.7m, t=0.26s:

F_val = Eq_instance.rmid2F(0.7, 0.26)

Find F values at R_mid values of 0.5m and 0.7m at the single time t=0.26s:

F_arr = Eq_instance.rmid2F([0.5, 0.7], 0.26)

Find F values at R_mid=0.5m at times t=[0.2s, 0.3s]:

F_arr = Eq_instance.rmid2F(0.5, [0.2, 0.3])

Find F values at (R_mid, t) points (0.6m, 0.2s) and (0.5m, 0.3s):

F_arr = Eq_instance.rmid2F([0.6, 0.5], [0.2, 0.3], each_t=False)
roa2F(roa, t, **kwargs)[source]

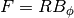Convert the passed (r/a, t) coordinates into the flux function F=RB_{\phi}.

By default, EFIT only computes this inside the LCFS.

Parameters:
  • roa (Array-like or scalar float) – Values of the normalized minor radius to map to F.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of roa. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as roa.
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of F. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in roa are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of roa or be a scalar. Default is True (evaluate ALL roa at EACH element in t).
  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • return_t (Boolean) – Set to True to return a tuple of (F, time_idxs), where time_idxs is the array of time indices actually used in evaluating F with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return F).
Returns:

F or (F, time_idxs)

  • F (Array or scalar float) - The flux function 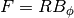F=RB_{\phi}. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as F) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single F value at r/a=0.6, t=0.26s:

F_val = Eq_instance.roa2F(0.6, 0.26)

Find F values at r/a points 0.6 and 0.8 at the single time t=0.26s.:

F_arr = Eq_instance.roa2F([0.6, 0.8], 0.26)

Find F values at r/a of 0.6 at times t=[0.2s, 0.3s]:

F_arr = Eq_instance.roa2F(0.6, [0.2, 0.3])

Find F values at (roa, t) points (0.6, 0.2s) and (0.5, 0.3s):

F_arr = Eq_instance.roa2F([0.6, 0.5], [0.2, 0.3], each_t=False)
psinorm2F(psinorm, t, **kwargs)[source]

Calculates the flux function 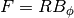F=RB_{\phi} corresponding to the passed psi_norm (normalized poloidal flux) values.

By default, EFIT only computes this inside the LCFS.

Parameters:
  • psi_norm (Array-like or scalar float) – Values of the normalized poloidal flux to map to F.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of psi_norm. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as psi_norm.
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of F. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in psi_norm are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of psi_norm or be a scalar. Default is True (evaluate ALL psi_norm at EACH element in t).
  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • return_t (Boolean) – Set to True to return a tuple of (F, time_idxs), where time_idxs is the array of time indices actually used in evaluating F with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return F).
Returns:

F or (F, time_idxs)

  • F (Array or scalar float) - The flux function 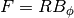F=RB_{\phi}. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as F) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single F value for psinorm=0.7, t=0.26s:

F_val = Eq_instance.psinorm2F(0.7, 0.26)

Find F values at psi_norm values of 0.5 and 0.7 at the single time t=0.26s:

F_arr = Eq_instance.psinorm2F([0.5, 0.7], 0.26)

Find F values at psi_norm=0.5 at times t=[0.2s, 0.3s]:

F_arr = Eq_instance.psinorm2F(0.5, [0.2, 0.3])

Find F values at (psinorm, t) points (0.6, 0.2s) and (0.5, 0.3s):

F_arr = Eq_instance.psinorm2F([0.6, 0.5], [0.2, 0.3], each_t=False)
phinorm2F(phinorm, t, **kwargs)[source]

Calculates the flux function 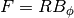F=RB_{\phi} corresponding to the passed phinorm (normalized toroidal flux) values.

By default, EFIT only computes this inside the LCFS.

Parameters:
  • phinorm (Array-like or scalar float) – Values of the normalized toroidal flux to map to F.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of phinorm. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as phinorm.
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of F. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in phinorm are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of phinorm or be a scalar. Default is True (evaluate ALL phinorm at EACH element in t).
  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • return_t (Boolean) – Set to True to return a tuple of (F, time_idxs), where time_idxs is the array of time indices actually used in evaluating F with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return F).
Returns:

F or (F, time_idxs)

  • F (Array or scalar float) - The flux function 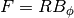F=RB_{\phi}. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as F) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single F value for phinorm=0.7, t=0.26s:

F_val = Eq_instance.phinorm2F(0.7, 0.26)

Find F values at phinorm values of 0.5 and 0.7 at the single time t=0.26s:

F_arr = Eq_instance.phinorm2F([0.5, 0.7], 0.26)

Find F values at phinorm=0.5 at times t=[0.2s, 0.3s]:

F_arr = Eq_instance.phinorm2F(0.5, [0.2, 0.3])

Find F values at (phinorm, t) points (0.6, 0.2s) and (0.5, 0.3s):

F_arr = Eq_instance.phinorm2F([0.6, 0.5], [0.2, 0.3], each_t=False)
volnorm2F(volnorm, t, **kwargs)[source]

Calculates the flux function 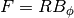F=RB_{\phi} corresponding to the passed volnorm (normalized flux surface volume) values.

By default, EFIT only computes this inside the LCFS.

Parameters:
  • volnorm (Array-like or scalar float) – Values of the normalized flux surface volume to map to F.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of volnorm. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as volnorm.
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of F. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in volnorm are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of volnorm or be a scalar. Default is True (evaluate ALL volnorm at EACH element in t).
  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • return_t (Boolean) – Set to True to return a tuple of (F, time_idxs), where time_idxs is the array of time indices actually used in evaluating F with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return F).
Returns:

F or (F, time_idxs)

  • F (Array or scalar float) - The flux function 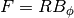F=RB_{\phi}. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as F) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single F value for volnorm=0.7, t=0.26s:

F_val = Eq_instance.volnorm2F(0.7, 0.26)

Find F values at volnorm values of 0.5 and 0.7 at the single time t=0.26s:

F_arr = Eq_instance.volnorm2F([0.5, 0.7], 0.26)

Find F values at volnorm=0.5 at times t=[0.2s, 0.3s]:

F_arr = Eq_instance.volnorm2F(0.5, [0.2, 0.3])

Find F values at (volnorm, t) points (0.6, 0.2s) and (0.5, 0.3s):

F_arr = Eq_instance.volnorm2F([0.6, 0.5], [0.2, 0.3], each_t=False)
Fnorm2psinorm(F, t, **kwargs)[source]

Calculates the psinorm (normalized poloidal flux) corresponding to the passed normalized flux function 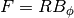F=RB_{\phi} values.

This is provided as a convenience method to plot current lines with the correct spacing: current lines launched from a grid uniformly-spaced in Fnorm will have spacing directly proportional to the magnitude.

By default, EFIT only computes this inside the LCFS. Furthermore, it is truncated at the radius at which is becomes non-monotonic.

Parameters:
  • F (Array-like or scalar float) – Values of F to map to psinorm.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of volnorm. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as volnorm.
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of psinorm. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in F are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of F or be a scalar. Default is True (evaluate ALL volnorm at EACH element in t).
  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • return_t (Boolean) – Set to True to return a tuple of (psinorm, time_idxs), where time_idxs is the array of time indices actually used in evaluating psinorm with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return psinorm).
Returns:

psinorm or (psinorm, time_idxs)

  • psinorm (Array or scalar float) - The normalized poloidal flux. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as psinorm) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single psinorm value for F=0.7, t=0.26s:

psinorm_val = Eq_instance.F2psinorm(0.7, 0.26)

Find psinorm values at F values of 0.5 and 0.7 at the single time t=0.26s:

psinorm_arr = Eq_instance.F2psinorm([0.5, 0.7], 0.26)

Find psinorm values at F=0.5 at times t=[0.2s, 0.3s]:

psinorm_arr = Eq_instance.F2psinorm(0.5, [0.2, 0.3])

Find psinorm values at (F, t) points (0.6, 0.2s) and (0.5, 0.3s):

psinorm_arr = Eq_instance.F2psinorm([0.6, 0.5], [0.2, 0.3], each_t=False)
rz2FFPrime(R, Z, t, **kwargs)[source]

Calculates the flux function 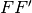FF' at the given (R, Z, t).

By default, EFIT only computes this inside the LCFS.

Parameters:
  • R (Array-like or scalar float) – Values of the radial coordinate to map to FFPrime. If R and Z are both scalar values, they are used as the coordinate pair for all of the values in t. Must have the same shape as Z unless the make_grid keyword is set. If the make_grid keyword is True, R must have exactly one dimension.
  • Z (Array-like or scalar float) – Values of the vertical coordinate to map to FFPrime. If R and Z are both scalar values, they are used as the coordinate pair for all of the values in t. Must have the same shape as R unless the make_grid keyword is set. If the make_grid keyword is True, Z must have exactly one dimension.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of R, Z. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as R and Z (or their meshgrid if make_grid is True).
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of FFPrime. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in R, Z are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of R and Z or be a scalar. Default is True (evaluate ALL R, Z at EACH element in t).
  • make_grid (Boolean) – Set to True to pass R and Z through scipy.meshgrid() before evaluating. If this is set to True, R and Z must each only have a single dimension, but can have different lengths. Default is False (do not form meshgrid).
  • length_unit (String or 1) –

    Length unit that R, Z are given in. If a string is given, it must be a valid unit specifier:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ meters

    If length_unit is 1 or None, meters are assumed. The default value is 1 (use meters).

  • return_t (Boolean) – Set to True to return a tuple of (FFPrime, time_idxs), where time_idxs is the array of time indices actually used in evaluating FFPrime with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return FFPrime).
Returns:

FFPrime or (FFPrime, time_idxs)

  • FFPrime (Array or scalar float) - The flux function 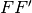FF'. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned. If R and Z both have the same shape then FFPrime has this shape as well, unless the make_grid keyword was True, in which case FFPrime has shape (len(Z), len(R)).
  • time_idxs (Array with same shape as FFPrime) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single FFPrime value at R=0.6m, Z=0.0m, t=0.26s:

FFPrime_val = Eq_instance.rz2FFPrime(0.6, 0, 0.26)

Find FFPrime values at (R, Z) points (0.6m, 0m) and (0.8m, 0m) at the single time t=0.26s. Note that the Z vector must be fully specified, even if the values are all the same:

FFPrime_arr = Eq_instance.rz2FFPrime([0.6, 0.8], [0, 0], 0.26)

Find FFPrime values at (R, Z) points (0.6m, 0m) at times t=[0.2s, 0.3s]:

FFPrime_arr = Eq_instance.rz2FFPrime(0.6, 0, [0.2, 0.3])

Find FFPrime values at (R, Z, t) points (0.6m, 0m, 0.2s) and (0.5m, 0.2m, 0.3s):

FFPrime_arr = Eq_instance.rz2FFPrime([0.6, 0.5], [0, 0.2], [0.2, 0.3], each_t=False)

Find FFPrime values on grid defined by 1D vector of radial positions R and 1D vector of vertical positions Z at time t=0.2s:

FFPrime_mat = Eq_instance.rz2FFPrime(R, Z, 0.2, make_grid=True)
rmid2FFPrime(R_mid, t, **kwargs)[source]

Calculates the flux function 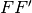FF' corresponding to the passed R_mid (mapped outboard midplane major radius) values.

By default, EFIT only computes this inside the LCFS.

Parameters:
  • R_mid (Array-like or scalar float) – Values of the outboard midplane major radius to map to FFPrime.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of R_mid. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as R_mid.
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of FFPrime. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in R_mid are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of R_mid or be a scalar. Default is True (evaluate ALL R_mid at EACH element in t).
  • length_unit (String or 1) –

    Length unit that R_mid is given in. If a string is given, it must be a valid unit specifier:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ meters

    If length_unit is 1 or None, meters are assumed. The default value is 1 (use meters).

  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • return_t (Boolean) – Set to True to return a tuple of (FFPrime, time_idxs), where time_idxs is the array of time indices actually used in evaluating FFPrime with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return FFPrime).
Returns:

FFPrime or (FFPrime, time_idxs)

  • FFPrime (Array or scalar float) - The flux function 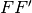FF'. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as FFPrime) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single FFPrime value for Rmid=0.7m, t=0.26s:

FFPrime_val = Eq_instance.rmid2FFPrime(0.7, 0.26)

Find FFPrime values at R_mid values of 0.5m and 0.7m at the single time t=0.26s:

FFPrime_arr = Eq_instance.rmid2FFPrime([0.5, 0.7], 0.26)

Find FFPrime values at R_mid=0.5m at times t=[0.2s, 0.3s]:

FFPrime_arr = Eq_instance.rmid2FFPrime(0.5, [0.2, 0.3])

Find FFPrime values at (R_mid, t) points (0.6m, 0.2s) and (0.5m, 0.3s):

FFPrime_arr = Eq_instance.rmid2FFPrime([0.6, 0.5], [0.2, 0.3], each_t=False)
roa2FFPrime(roa, t, **kwargs)[source]

Convert the passed (r/a, t) coordinates into the flux function FF'.

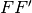By default, EFIT only computes this inside the LCFS.

Parameters:
  • roa (Array-like or scalar float) – Values of the normalized minor radius to map to FFPrime.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of roa. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as roa.
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of FFPrime. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in roa are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of roa or be a scalar. Default is True (evaluate ALL roa at EACH element in t).
  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • return_t (Boolean) – Set to True to return a tuple of (FFPrime, time_idxs), where time_idxs is the array of time indices actually used in evaluating FFPrime with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return FFPrime).
Returns:

FFPrime or (FFPrime, time_idxs)

  • FFPrime (Array or scalar float) - The flux function 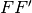FF'. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as FFPrime) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single FFPrime value at r/a=0.6, t=0.26s:

FFPrime_val = Eq_instance.roa2FFPrime(0.6, 0.26)

Find FFPrime values at r/a points 0.6 and 0.8 at the single time t=0.26s.:

FFPrime_arr = Eq_instance.roa2FFPrime([0.6, 0.8], 0.26)

Find FFPrime values at r/a of 0.6 at times t=[0.2s, 0.3s]:

FFPrime_arr = Eq_instance.roa2FFPrime(0.6, [0.2, 0.3])

Find FFPrime values at (roa, t) points (0.6, 0.2s) and (0.5, 0.3s):

FFPrime_arr = Eq_instance.roa2FFPrime([0.6, 0.5], [0.2, 0.3], each_t=False)
psinorm2FFPrime(psinorm, t, **kwargs)[source]

Calculates the flux function 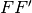FF' corresponding to the passed psi_norm (normalized poloidal flux) values.

By default, EFIT only computes this inside the LCFS.

Parameters:
  • psi_norm (Array-like or scalar float) – Values of the normalized poloidal flux to map to FFPrime.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of psi_norm. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as psi_norm.
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of FFPrime. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in psi_norm are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of psi_norm or be a scalar. Default is True (evaluate ALL psi_norm at EACH element in t).
  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • return_t (Boolean) – Set to True to return a tuple of (FFPrime, time_idxs), where time_idxs is the array of time indices actually used in evaluating FFPrime with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return FFPrime).
Returns:

FFPrime or (FFPrime, time_idxs)

  • FFPrime (Array or scalar float) - The flux function 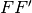FF'. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as FFPrime) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single FFPrime value for psinorm=0.7, t=0.26s:

FFPrime_val = Eq_instance.psinorm2FFPrime(0.7, 0.26)

Find FFPrime values at psi_norm values of 0.5 and 0.7 at the single time t=0.26s:

FFPrime_arr = Eq_instance.psinorm2FFPrime([0.5, 0.7], 0.26)

Find FFPrime values at psi_norm=0.5 at times t=[0.2s, 0.3s]:

FFPrime_arr = Eq_instance.psinorm2FFPrime(0.5, [0.2, 0.3])

Find FFPrime values at (psinorm, t) points (0.6, 0.2s) and (0.5, 0.3s):

FFPrime_arr = Eq_instance.psinorm2FFPrime([0.6, 0.5], [0.2, 0.3], each_t=False)
phinorm2FFPrime(phinorm, t, **kwargs)[source]

Calculates the flux function 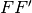FF' corresponding to the passed phinorm (normalized toroidal flux) values.

By default, EFIT only computes this inside the LCFS.

Parameters:
  • phinorm (Array-like or scalar float) – Values of the normalized toroidal flux to map to FFPrime.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of phinorm. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as phinorm.
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of FFPrime. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in phinorm are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of phinorm or be a scalar. Default is True (evaluate ALL phinorm at EACH element in t).
  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • return_t (Boolean) – Set to True to return a tuple of (FFPrime, time_idxs), where time_idxs is the array of time indices actually used in evaluating FFPrime with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return FFPrime).
Returns:

FFPrime or (FFPrime, time_idxs)

  • FFPrime (Array or scalar float) - The flux function 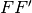FF'. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as FFPrime) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single FFPrime value for phinorm=0.7, t=0.26s:

FFPrime_val = Eq_instance.phinorm2FFPrime(0.7, 0.26)

Find FFPrime values at phinorm values of 0.5 and 0.7 at the single time t=0.26s:

FFPrime_arr = Eq_instance.phinorm2FFPrime([0.5, 0.7], 0.26)

Find FFPrime values at phinorm=0.5 at times t=[0.2s, 0.3s]:

FFPrime_arr = Eq_instance.phinorm2FFPrime(0.5, [0.2, 0.3])

Find FFPrime values at (phinorm, t) points (0.6, 0.2s) and (0.5, 0.3s):

FFPrime_arr = Eq_instance.phinorm2FFPrime([0.6, 0.5], [0.2, 0.3], each_t=False)
volnorm2FFPrime(volnorm, t, **kwargs)[source]

Calculates the flux function 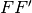FF' corresponding to the passed volnorm (normalized flux surface volume) values.

By default, EFIT only computes this inside the LCFS.

Parameters:
  • volnorm (Array-like or scalar float) – Values of the normalized flux surface volume to map to FFPrime.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of volnorm. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as volnorm.
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of FFPrime. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in volnorm are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of volnorm or be a scalar. Default is True (evaluate ALL volnorm at EACH element in t).
  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • return_t (Boolean) – Set to True to return a tuple of (FFPrime, time_idxs), where time_idxs is the array of time indices actually used in evaluating FFPrime with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return FFPrime).
Returns:

FFPrime or (FFPrime, time_idxs)

  • FFPrime (Array or scalar float) - The flux function 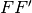FF'. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as FFPrime) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single FFPrime value for volnorm=0.7, t=0.26s:

FFPrime_val = Eq_instance.volnorm2FFPrime(0.7, 0.26)

Find FFPrime values at volnorm values of 0.5 and 0.7 at the single time t=0.26s:

FFPrime_arr = Eq_instance.volnorm2FFPrime([0.5, 0.7], 0.26)

Find FFPrime values at volnorm=0.5 at times t=[0.2s, 0.3s]:

FFPrime_arr = Eq_instance.volnorm2FFPrime(0.5, [0.2, 0.3])

Find FFPrime values at (volnorm, t) points (0.6, 0.2s) and (0.5, 0.3s):

FFPrime_arr = Eq_instance.volnorm2FFPrime([0.6, 0.5], [0.2, 0.3], each_t=False)
rz2p(R, Z, t, **kwargs)[source]

Calculates the pressure at the given (R, Z, t).

By default, EFIT only computes this inside the LCFS.

Parameters:
  • R (Array-like or scalar float) – Values of the radial coordinate to map to p. If R and Z are both scalar values, they are used as the coordinate pair for all of the values in t. Must have the same shape as Z unless the make_grid keyword is set. If the make_grid keyword is True, R must have exactly one dimension.
  • Z (Array-like or scalar float) – Values of the vertical coordinate to map to p. If R and Z are both scalar values, they are used as the coordinate pair for all of the values in t. Must have the same shape as R unless the make_grid keyword is set. If the make_grid keyword is True, Z must have exactly one dimension.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of R, Z. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as R and Z (or their meshgrid if make_grid is True).
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of p. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in R, Z are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of R and Z or be a scalar. Default is True (evaluate ALL R, Z at EACH element in t).
  • make_grid (Boolean) – Set to True to pass R and Z through scipy.meshgrid() before evaluating. If this is set to True, R and Z must each only have a single dimension, but can have different lengths. Default is False (do not form meshgrid).
  • length_unit (String or 1) –

    Length unit that R, Z are given in. If a string is given, it must be a valid unit specifier:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ meters

    If length_unit is 1 or None, meters are assumed. The default value is 1 (use meters).

  • return_t (Boolean) – Set to True to return a tuple of (p, time_idxs), where time_idxs is the array of time indices actually used in evaluating p with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return p).
Returns:

p or (p, time_idxs)

  • p (Array or scalar float) - The pressure. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned. If R and Z both have the same shape then p has this shape as well, unless the make_grid keyword was True, in which case p has shape (len(Z), len(R)).
  • time_idxs (Array with same shape as p) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single p value at R=0.6m, Z=0.0m, t=0.26s:

p_val = Eq_instance.rz2p(0.6, 0, 0.26)

Find p values at (R, Z) points (0.6m, 0m) and (0.8m, 0m) at the single time t=0.26s. Note that the Z vector must be fully specified, even if the values are all the same:

p_arr = Eq_instance.rz2p([0.6, 0.8], [0, 0], 0.26)

Find p values at (R, Z) points (0.6m, 0m) at times t=[0.2s, 0.3s]:

p_arr = Eq_instance.rz2p(0.6, 0, [0.2, 0.3])

Find p values at (R, Z, t) points (0.6m, 0m, 0.2s) and (0.5m, 0.2m, 0.3s):

p_arr = Eq_instance.rz2p([0.6, 0.5], [0, 0.2], [0.2, 0.3], each_t=False)

Find p values on grid defined by 1D vector of radial positions R and 1D vector of vertical positions Z at time t=0.2s:

p_mat = Eq_instance.rz2p(R, Z, 0.2, make_grid=True)
rmid2p(R_mid, t, **kwargs)[source]

Calculates the pressure corresponding to the passed R_mid (mapped outboard midplane major radius) values.

By default, EFIT only computes this inside the LCFS.

Parameters:
  • R_mid (Array-like or scalar float) – Values of the outboard midplane major radius to map to p.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of R_mid. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as R_mid.
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of p. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in R_mid are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of R_mid or be a scalar. Default is True (evaluate ALL R_mid at EACH element in t).
  • length_unit (String or 1) –

    Length unit that R_mid is given in. If a string is given, it must be a valid unit specifier:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ meters

    If length_unit is 1 or None, meters are assumed. The default value is 1 (use meters).

  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • return_t (Boolean) – Set to True to return a tuple of (p, time_idxs), where time_idxs is the array of time indices actually used in evaluating p with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return p).
Returns:

p or (p, time_idxs)

  • p (Array or scalar float) - The pressure. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as p) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single p value for Rmid=0.7m, t=0.26s:

p_val = Eq_instance.rmid2p(0.7, 0.26)

Find p values at R_mid values of 0.5m and 0.7m at the single time t=0.26s:

p_arr = Eq_instance.rmid2p([0.5, 0.7], 0.26)

Find p values at R_mid=0.5m at times t=[0.2s, 0.3s]:

p_arr = Eq_instance.rmid2p(0.5, [0.2, 0.3])

Find p values at (R_mid, t) points (0.6m, 0.2s) and (0.5m, 0.3s):

p_arr = Eq_instance.rmid2p([0.6, 0.5], [0.2, 0.3], each_t=False)
roa2p(roa, t, **kwargs)[source]

Convert the passed (r/a, t) coordinates into pressure.

By default, EFIT only computes this inside the LCFS.

Parameters:
  • roa (Array-like or scalar float) – Values of the normalized minor radius to map to p.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of roa. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as roa.
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of p. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in roa are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of roa or be a scalar. Default is True (evaluate ALL roa at EACH element in t).
  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • return_t (Boolean) – Set to True to return a tuple of (p, time_idxs), where time_idxs is the array of time indices actually used in evaluating p with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return p).
Returns:

p or (p, time_idxs)

  • p (Array or scalar float) - The pressure. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as p) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single p value at r/a=0.6, t=0.26s:

p_val = Eq_instance.roa2p(0.6, 0.26)

Find p values at r/a points 0.6 and 0.8 at the single time t=0.26s.:

p_arr = Eq_instance.roa2p([0.6, 0.8], 0.26)

Find p values at r/a of 0.6 at times t=[0.2s, 0.3s]:

p_arr = Eq_instance.roa2p(0.6, [0.2, 0.3])

Find p values at (roa, t) points (0.6, 0.2s) and (0.5, 0.3s):

p_arr = Eq_instance.roa2p([0.6, 0.5], [0.2, 0.3], each_t=False)
psinorm2p(psinorm, t, **kwargs)[source]

Calculates the pressure corresponding to the passed psi_norm (normalized poloidal flux) values.

By default, EFIT only computes this inside the LCFS.

Parameters:
  • psi_norm (Array-like or scalar float) – Values of the normalized poloidal flux to map to p.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of psi_norm. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as psi_norm.
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of p. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in psi_norm are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of psi_norm or be a scalar. Default is True (evaluate ALL psi_norm at EACH element in t).
  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • return_t (Boolean) – Set to True to return a tuple of (p, time_idxs), where time_idxs is the array of time indices actually used in evaluating p with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return p).
Returns:

p or (p, time_idxs)

  • p (Array or scalar float) - The pressure. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as p) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single p value for psinorm=0.7, t=0.26s:

p_val = Eq_instance.psinorm2p(0.7, 0.26)

Find p values at psi_norm values of 0.5 and 0.7 at the single time t=0.26s:

p_arr = Eq_instance.psinorm2p([0.5, 0.7], 0.26)

Find p values at psi_norm=0.5 at times t=[0.2s, 0.3s]:

p_arr = Eq_instance.psinorm2p(0.5, [0.2, 0.3])

Find p values at (psinorm, t) points (0.6, 0.2s) and (0.5, 0.3s):

p_arr = Eq_instance.psinorm2p([0.6, 0.5], [0.2, 0.3], each_t=False)
phinorm2p(phinorm, t, **kwargs)[source]

Calculates the pressure corresponding to the passed phinorm (normalized toroidal flux) values.

By default, EFIT only computes this inside the LCFS.

Parameters:
  • phinorm (Array-like or scalar float) – Values of the normalized toroidal flux to map to p.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of phinorm. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as phinorm.
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of p. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in phinorm are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of phinorm or be a scalar. Default is True (evaluate ALL phinorm at EACH element in t).
  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • return_t (Boolean) – Set to True to return a tuple of (p, time_idxs), where time_idxs is the array of time indices actually used in evaluating p with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return p).
Returns:

p or (p, time_idxs)

  • p (Array or scalar float) - The pressure. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as p) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single p value for phinorm=0.7, t=0.26s:

p_val = Eq_instance.phinorm2p(0.7, 0.26)

Find p values at phinorm values of 0.5 and 0.7 at the single time t=0.26s:

p_arr = Eq_instance.phinorm2p([0.5, 0.7], 0.26)

Find p values at phinorm=0.5 at times t=[0.2s, 0.3s]:

p_arr = Eq_instance.phinorm2p(0.5, [0.2, 0.3])

Find p values at (phinorm, t) points (0.6, 0.2s) and (0.5, 0.3s):

p_arr = Eq_instance.phinorm2p([0.6, 0.5], [0.2, 0.3], each_t=False)
volnorm2p(volnorm, t, **kwargs)[source]

Calculates the pressure corresponding to the passed volnorm (normalized flux surface volume) values.

By default, EFIT only computes this inside the LCFS.

Parameters:
  • volnorm (Array-like or scalar float) – Values of the normalized flux surface volume to map to p.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of volnorm. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as volnorm.
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of p. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in volnorm are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of volnorm or be a scalar. Default is True (evaluate ALL volnorm at EACH element in t).
  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • return_t (Boolean) – Set to True to return a tuple of (p, time_idxs), where time_idxs is the array of time indices actually used in evaluating p with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return p).
Returns:

p or (p, time_idxs)

  • p (Array or scalar float) - The pressure. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as p) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single p value for volnorm=0.7, t=0.26s:

p_val = Eq_instance.volnorm2p(0.7, 0.26)

Find p values at volnorm values of 0.5 and 0.7 at the single time t=0.26s:

p_arr = Eq_instance.volnorm2p([0.5, 0.7], 0.26)

Find p values at volnorm=0.5 at times t=[0.2s, 0.3s]:

p_arr = Eq_instance.volnorm2p(0.5, [0.2, 0.3])

Find p values at (volnorm, t) points (0.6, 0.2s) and (0.5, 0.3s):

p_arr = Eq_instance.volnorm2p([0.6, 0.5], [0.2, 0.3], each_t=False)
rz2pprime(R, Z, t, **kwargs)[source]

Calculates the pressure gradient at the given (R, Z, t).

By default, EFIT only computes this inside the LCFS.

Parameters:
  • R (Array-like or scalar float) – Values of the radial coordinate to map to pprime. If R and Z are both scalar values, they are used as the coordinate pair for all of the values in t. Must have the same shape as Z unless the make_grid keyword is set. If the make_grid keyword is True, R must have exactly one dimension.
  • Z (Array-like or scalar float) – Values of the vertical coordinate to map to pprime. If R and Z are both scalar values, they are used as the coordinate pair for all of the values in t. Must have the same shape as R unless the make_grid keyword is set. If the make_grid keyword is True, Z must have exactly one dimension.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of R, Z. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as R and Z (or their meshgrid if make_grid is True).
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of pprime. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in R, Z are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of R and Z or be a scalar. Default is True (evaluate ALL R, Z at EACH element in t).
  • make_grid (Boolean) – Set to True to pass R and Z through scipy.meshgrid() before evaluating. If this is set to True, R and Z must each only have a single dimension, but can have different lengths. Default is False (do not form meshgrid).
  • length_unit (String or 1) –

    Length unit that R, Z are given in. If a string is given, it must be a valid unit specifier:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ meters

    If length_unit is 1 or None, meters are assumed. The default value is 1 (use meters).

  • return_t (Boolean) – Set to True to return a tuple of (pprime, time_idxs), where time_idxs is the array of time indices actually used in evaluating pprime with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return pprime).
Returns:

pprime or (pprime, time_idxs)

  • pprime (Array or scalar float) - The pressure gradient. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned. If R and Z both have the same shape then p has this shape as well, unless the make_grid keyword was True, in which case p has shape (len(Z), len(R)).
  • time_idxs (Array with same shape as pprime) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single pprime value at R=0.6m, Z=0.0m, t=0.26s:

pprime_val = Eq_instance.rz2pprime(0.6, 0, 0.26)

Find pprime values at (R, Z) points (0.6m, 0m) and (0.8m, 0m) at the single time t=0.26s. Note that the Z vector must be fully specified, even if the values are all the same:

pprime_arr = Eq_instance.rz2pprime([0.6, 0.8], [0, 0], 0.26)

Find pprime values at (R, Z) points (0.6m, 0m) at times t=[0.2s, 0.3s]:

pprime_arr = Eq_instance.rz2pprime(0.6, 0, [0.2, 0.3])

Find pprime values at (R, Z, t) points (0.6m, 0m, 0.2s) and (0.5m, 0.2m, 0.3s):

pprime_arr = Eq_instance.rz2pprime([0.6, 0.5], [0, 0.2], [0.2, 0.3], each_t=False)

Find pprime values on grid defined by 1D vector of radial positions R and 1D vector of vertical positions Z at time t=0.2s:

pprime_mat = Eq_instance.rz2pprime(R, Z, 0.2, make_grid=True)
rmid2pprime(R_mid, t, **kwargs)[source]

Calculates the pressure gradient corresponding to the passed R_mid (mapped outboard midplane major radius) values.

By default, EFIT only computes this inside the LCFS.

Parameters:
  • R_mid (Array-like or scalar float) – Values of the outboard midplane major radius to map to pprime.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of R_mid. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as R_mid.
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of pprime. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in R_mid are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of R_mid or be a scalar. Default is True (evaluate ALL R_mid at EACH element in t).
  • length_unit (String or 1) –

    Length unit that R_mid is given in. If a string is given, it must be a valid unit specifier:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ meters

    If length_unit is 1 or None, meters are assumed. The default value is 1 (use meters).

  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • return_t (Boolean) – Set to True to return a tuple of (pprime, time_idxs), where time_idxs is the array of time indices actually used in evaluating pprime with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return pprime).
Returns:

pprime or (pprime, time_idxs)

  • pprime (Array or scalar float) - The pressure gradient. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as pprime) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single pprime value for Rmid=0.7m, t=0.26s:

pprime_val = Eq_instance.rmid2pprime(0.7, 0.26)

Find pprime values at R_mid values of 0.5m and 0.7m at the single time t=0.26s:

pprime_arr = Eq_instance.rmid2pprime([0.5, 0.7], 0.26)

Find pprime values at R_mid=0.5m at times t=[0.2s, 0.3s]:

pprime_arr = Eq_instance.rmid2pprime(0.5, [0.2, 0.3])

Find pprime values at (R_mid, t) points (0.6m, 0.2s) and (0.5m, 0.3s):

pprime_arr = Eq_instance.rmid2pprime([0.6, 0.5], [0.2, 0.3], each_t=False)
roa2pprime(roa, t, **kwargs)[source]

Convert the passed (r/a, t) coordinates into pressure gradient.

By default, EFIT only computes this inside the LCFS.

Parameters:
  • roa (Array-like or scalar float) – Values of the normalized minor radius to map to pprime.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of roa. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as roa.
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of pprime. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in roa are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of roa or be a scalar. Default is True (evaluate ALL roa at EACH element in t).
  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • return_t (Boolean) – Set to True to return a tuple of (pprime, time_idxs), where time_idxs is the array of time indices actually used in evaluating pprime with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return pprime).
Returns:

pprime or (pprime, time_idxs)

  • pprime (Array or scalar float) - The pressure gradient. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as pprime) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single pprime value at r/a=0.6, t=0.26s:

pprime_val = Eq_instance.roa2pprime(0.6, 0.26)

Find pprime values at r/a points 0.6 and 0.8 at the single time t=0.26s.:

pprime_arr = Eq_instance.roa2pprime([0.6, 0.8], 0.26)

Find pprime values at r/a of 0.6 at times t=[0.2s, 0.3s]:

pprime_arr = Eq_instance.roa2pprime(0.6, [0.2, 0.3])

Find pprime values at (roa, t) points (0.6, 0.2s) and (0.5, 0.3s):

pprime_arr = Eq_instance.roa2pprime([0.6, 0.5], [0.2, 0.3], each_t=False)
psinorm2pprime(psinorm, t, **kwargs)[source]

Calculates the pressure gradient corresponding to the passed psi_norm (normalized poloidal flux) values.

By default, EFIT only computes this inside the LCFS.

Parameters:
  • psi_norm (Array-like or scalar float) – Values of the normalized poloidal flux to map to pprime.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of psi_norm. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as psi_norm.
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of pprime. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in psi_norm are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of psi_norm or be a scalar. Default is True (evaluate ALL psi_norm at EACH element in t).
  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • return_t (Boolean) – Set to True to return a tuple of (pprime, time_idxs), where time_idxs is the array of time indices actually used in evaluating pprime with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return pprime).
Returns:

pprime or (pprime, time_idxs)

  • pprime (Array or scalar float) - The pressure gradient. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as pprime) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single pprime value for psinorm=0.7, t=0.26s:

pprime_val = Eq_instance.psinorm2pprime(0.7, 0.26)

Find pprime values at psi_norm values of 0.5 and 0.7 at the single time t=0.26s:

pprime_arr = Eq_instance.psinorm2pprime([0.5, 0.7], 0.26)

Find pprime values at psi_norm=0.5 at times t=[0.2s, 0.3s]:

pprime_arr = Eq_instance.psinorm2pprime(0.5, [0.2, 0.3])

Find pprime values at (psinorm, t) points (0.6, 0.2s) and (0.5, 0.3s):

pprime_arr = Eq_instance.psinorm2pprime([0.6, 0.5], [0.2, 0.3], each_t=False)
phinorm2pprime(phinorm, t, **kwargs)[source]

Calculates the pressure gradient corresponding to the passed phinorm (normalized toroidal flux) values.

By default, EFIT only computes this inside the LCFS.

Parameters:
  • phinorm (Array-like or scalar float) – Values of the normalized toroidal flux to map to pprime.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of phinorm. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as phinorm.
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of pprime. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in phinorm are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of phinorm or be a scalar. Default is True (evaluate ALL phinorm at EACH element in t).
  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • return_t (Boolean) – Set to True to return a tuple of (pprime, time_idxs), where time_idxs is the array of time indices actually used in evaluating pprime with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return pprime).
Returns:

pprime or (pprime, time_idxs)

  • pprime (Array or scalar float) - The pressure gradient. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as pprime) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single pprime value for phinorm=0.7, t=0.26s:

pprime_val = Eq_instance.phinorm2pprime(0.7, 0.26)

Find pprime values at phinorm values of 0.5 and 0.7 at the single time t=0.26s:

pprime_arr = Eq_instance.phinorm2pprime([0.5, 0.7], 0.26)

Find pprime values at phinorm=0.5 at times t=[0.2s, 0.3s]:

pprime_arr = Eq_instance.phinorm2pprime(0.5, [0.2, 0.3])

Find pprime values at (phinorm, t) points (0.6, 0.2s) and (0.5, 0.3s):

pprime_arr = Eq_instance.phinorm2pprime([0.6, 0.5], [0.2, 0.3], each_t=False)
volnorm2pprime(volnorm, t, **kwargs)[source]

Calculates the pressure gradient corresponding to the passed volnorm (normalized flux surface volume) values.

By default, EFIT only computes this inside the LCFS.

Parameters:
  • volnorm (Array-like or scalar float) – Values of the normalized flux surface volume to map to pprime.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of volnorm. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as volnorm.
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of pprime. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in volnorm are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of volnorm or be a scalar. Default is True (evaluate ALL volnorm at EACH element in t).
  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • return_t (Boolean) – Set to True to return a tuple of (pprime, time_idxs), where time_idxs is the array of time indices actually used in evaluating pprime with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return pprime).
Returns:

pprime or (pprime, time_idxs)

  • pprime (Array or scalar float) - The pressure gradient. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as pprime) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single pprime value for volnorm=0.7, t=0.26s:

pprime_val = Eq_instance.volnorm2pprime(0.7, 0.26)

Find pprime values at volnorm values of 0.5 and 0.7 at the single time t=0.26s:

pprime_arr = Eq_instance.volnorm2pprime([0.5, 0.7], 0.26)

Find pprime values at volnorm=0.5 at times t=[0.2s, 0.3s]:

pprime_arr = Eq_instance.volnorm2pprime(0.5, [0.2, 0.3])

Find pprime values at (volnorm, t) points (0.6, 0.2s) and (0.5, 0.3s):

pprime_arr = Eq_instance.volnorm2pprime([0.6, 0.5], [0.2, 0.3], each_t=False)
rz2v(R, Z, t, **kwargs)[source]

Calculates the flux surface volume at the given (R, Z, t).

By default, EFIT only computes this inside the LCFS.

Parameters:
  • R (Array-like or scalar float) – Values of the radial coordinate to map to v. If R and Z are both scalar values, they are used as the coordinate pair for all of the values in t. Must have the same shape as Z unless the make_grid keyword is set. If the make_grid keyword is True, R must have exactly one dimension.
  • Z (Array-like or scalar float) – Values of the vertical coordinate to map to v. If R and Z are both scalar values, they are used as the coordinate pair for all of the values in t. Must have the same shape as R unless the make_grid keyword is set. If the make_grid keyword is True, Z must have exactly one dimension.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of R, Z. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as R and Z (or their meshgrid if make_grid is True).
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of v. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in R, Z are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of R and Z or be a scalar. Default is True (evaluate ALL R, Z at EACH element in t).
  • make_grid (Boolean) – Set to True to pass R and Z through scipy.meshgrid() before evaluating. If this is set to True, R and Z must each only have a single dimension, but can have different lengths. Default is False (do not form meshgrid).
  • length_unit (String or 1) –

    Length unit that R, Z are given in. If a string is given, it must be a valid unit specifier:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ meters

    If length_unit is 1 or None, meters are assumed. The default value is 1 (use meters).

  • return_t (Boolean) – Set to True to return a tuple of (v, time_idxs), where time_idxs is the array of time indices actually used in evaluating v with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return v).
Returns:

v or (v, time_idxs)

  • v (Array or scalar float) - The flux surface volume. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned. If R and Z both have the same shape then v has this shape as well, unless the make_grid keyword was True, in which case v has shape (len(Z), len(R)).
  • time_idxs (Array with same shape as v) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single v value at R=0.6m, Z=0.0m, t=0.26s:

v_val = Eq_instance.rz2v(0.6, 0, 0.26)

Find v values at (R, Z) points (0.6m, 0m) and (0.8m, 0m) at the single time t=0.26s. Note that the Z vector must be fully specified, even if the values are all the same:

v_arr = Eq_instance.rz2v([0.6, 0.8], [0, 0], 0.26)

Find v values at (R, Z) points (0.6m, 0m) at times t=[0.2s, 0.3s]:

v_arr = Eq_instance.rz2v(0.6, 0, [0.2, 0.3])

Find v values at (R, Z, t) points (0.6m, 0m, 0.2s) and (0.5m, 0.2m, 0.3s):

v_arr = Eq_instance.rz2v([0.6, 0.5], [0, 0.2], [0.2, 0.3], each_t=False)

Find v values on grid defined by 1D vector of radial positions R and 1D vector of vertical positions Z at time t=0.2s:

v_mat = Eq_instance.rz2v(R, Z, 0.2, make_grid=True)
rmid2v(R_mid, t, **kwargs)[source]

Calculates the flux surface volume corresponding to the passed R_mid (mapped outboard midplane major radius) values.

By default, EFIT only computes this inside the LCFS.

Parameters:
  • R_mid (Array-like or scalar float) – Values of the outboard midplane major radius to map to v.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of R_mid. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as R_mid.
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of v. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in R_mid are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of R_mid or be a scalar. Default is True (evaluate ALL R_mid at EACH element in t).
  • length_unit (String or 1) –

    Length unit that R_mid is given in. If a string is given, it must be a valid unit specifier:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ meters

    If length_unit is 1 or None, meters are assumed. The default value is 1 (use meters).

  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • return_t (Boolean) – Set to True to return a tuple of (p, time_idxs), where time_idxs is the array of time indices actually used in evaluating p with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return p).
Returns:

v or (v, time_idxs)

  • v (Array or scalar float) - The flux surface volume. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as v) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single v value for Rmid=0.7m, t=0.26s:

v_val = Eq_instance.rmid2v(0.7, 0.26)

Find v values at R_mid values of 0.5m and 0.7m at the single time t=0.26s:

v_arr = Eq_instance.rmid2v([0.5, 0.7], 0.26)

Find v values at R_mid=0.5m at times t=[0.2s, 0.3s]:

v_arr = Eq_instance.rmid2v(0.5, [0.2, 0.3])

Find v values at (R_mid, t) points (0.6m, 0.2s) and (0.5m, 0.3s):

v_arr = Eq_instance.rmid2v([0.6, 0.5], [0.2, 0.3], each_t=False)
roa2v(roa, t, **kwargs)[source]

Convert the passed (r/a, t) coordinates into flux surface volume.

By default, EFIT only computes this inside the LCFS.

Parameters:
  • roa (Array-like or scalar float) – Values of the normalized minor radius to map to v.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of roa. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as roa.
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of v. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in roa are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of roa or be a scalar. Default is True (evaluate ALL roa at EACH element in t).
  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • return_t (Boolean) – Set to True to return a tuple of (v, time_idxs), where time_idxs is the array of time indices actually used in evaluating v with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return v).
Returns:

v or (v, time_idxs)

  • v (Array or scalar float) - The flux surface volume. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as v) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single v value at r/a=0.6, t=0.26s:

v_val = Eq_instance.roa2v(0.6, 0.26)

Find v values at r/a points 0.6 and 0.8 at the single time t=0.26s.:

v_arr = Eq_instance.roa2v([0.6, 0.8], 0.26)

Find v values at r/a of 0.6 at times t=[0.2s, 0.3s]:

v_arr = Eq_instance.roa2v(0.6, [0.2, 0.3])

Find v values at (roa, t) points (0.6, 0.2s) and (0.5, 0.3s):

v_arr = Eq_instance.roa2v([0.6, 0.5], [0.2, 0.3], each_t=False)
psinorm2v(psinorm, t, **kwargs)[source]

Calculates the flux surface volume corresponding to the passed psi_norm (normalized poloidal flux) values.

By default, EFIT only computes this inside the LCFS.

Parameters:
  • psi_norm (Array-like or scalar float) – Values of the normalized poloidal flux to map to v.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of psi_norm. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as psi_norm.
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of v. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in psi_norm are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of psi_norm or be a scalar. Default is True (evaluate ALL psi_norm at EACH element in t).
  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • return_t (Boolean) – Set to True to return a tuple of (v, time_idxs), where time_idxs is the array of time indices actually used in evaluating v with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return v).
Returns:

v or (v, time_idxs)

  • v (Array or scalar float) - The pressure. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as v) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single v value for psinorm=0.7, t=0.26s:

v_val = Eq_instance.psinorm2v(0.7, 0.26)

Find v values at psi_norm values of 0.5 and 0.7 at the single time t=0.26s:

v_arr = Eq_instance.psinorm2v([0.5, 0.7], 0.26)

Find v values at psi_norm=0.5 at times t=[0.2s, 0.3s]:

v_arr = Eq_instance.psinorm2v(0.5, [0.2, 0.3])

Find v values at (psinorm, t) points (0.6, 0.2s) and (0.5, 0.3s):

v_arr = Eq_instance.psinorm2v([0.6, 0.5], [0.2, 0.3], each_t=False)
phinorm2v(phinorm, t, **kwargs)[source]

Calculates the flux surface volume corresponding to the passed phinorm (normalized toroidal flux) values.

By default, EFIT only computes this inside the LCFS.

Parameters:
  • phinorm (Array-like or scalar float) – Values of the normalized toroidal flux to map to v.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of phinorm. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as phinorm.
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of v. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in phinorm are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of phinorm or be a scalar. Default is True (evaluate ALL phinorm at EACH element in t).
  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • return_t (Boolean) – Set to True to return a tuple of (v, time_idxs), where time_idxs is the array of time indices actually used in evaluating v with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return v).
Returns:

v or (v, time_idxs)

  • v (Array or scalar float) - The flux surface volume. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as v) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single v value for phinorm=0.7, t=0.26s:

v_val = Eq_instance.phinorm2v(0.7, 0.26)

Find v values at phinorm values of 0.5 and 0.7 at the single time t=0.26s:

v_arr = Eq_instance.phinorm2v([0.5, 0.7], 0.26)

Find v values at phinorm=0.5 at times t=[0.2s, 0.3s]:

v_arr = Eq_instance.phinorm2v(0.5, [0.2, 0.3])

Find v values at (phinorm, t) points (0.6, 0.2s) and (0.5, 0.3s):

v_arr = Eq_instance.phinorm2v([0.6, 0.5], [0.2, 0.3], each_t=False)
volnorm2v(volnorm, t, **kwargs)[source]

Calculates the flux surface volume corresponding to the passed volnorm (normalized flux surface volume) values.

By default, EFIT only computes this inside the LCFS.

Parameters:
  • volnorm (Array-like or scalar float) – Values of the normalized flux surface volume to map to v.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of volnorm. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as volnorm.
Keyword Arguments:
 
  • sqrt (Boolean) – Set to True to return the square root of v. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False.
  • each_t (Boolean) – When True, the elements in volnorm are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of volnorm or be a scalar. Default is True (evaluate ALL volnorm at EACH element in t).
  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • return_t (Boolean) – Set to True to return a tuple of (v, time_idxs), where time_idxs is the array of time indices actually used in evaluating v with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return v).
Returns:

v or (v, time_idxs)

  • v (Array or scalar float) - The flux surface volume. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned.
  • time_idxs (Array with same shape as v) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single v value for volnorm=0.7, t=0.26s:

v_val = Eq_instance.volnorm2p(0.7, 0.26)

Find v values at volnorm values of 0.5 and 0.7 at the single time t=0.26s:

v_arr = Eq_instance.volnorm2v([0.5, 0.7], 0.26)

Find v values at volnorm=0.5 at times t=[0.2s, 0.3s]:

v_arr = Eq_instance.volnorm2v(0.5, [0.2, 0.3])

Find v values at (volnorm, t) points (0.6, 0.2s) and (0.5, 0.3s):

v_arr = Eq_instance.volnorm2v([0.6, 0.5], [0.2, 0.3], each_t=False)
rz2BR(R, Z, t, return_t=False, make_grid=False, each_t=True, length_unit=1)[source]

Calculates the major radial component of the magnetic field at the given (R, Z, t) coordinates.

Uses

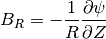
B_R = -\frac{1}{R}\frac{\partial \psi}{\partial Z}

Parameters:
  • R (Array-like or scalar float) – Values of the radial coordinate to map to radial field. If R and Z are both scalar values, they are used as the coordinate pair for all of the values in t. Must have the same shape as Z unless the make_grid keyword is set. If the make_grid keyword is True, R must have exactly one dimension.
  • Z (Array-like or scalar float) – Values of the vertical coordinate to map to radial field. If R and Z are both scalar values, they are used as the coordinate pair for all of the values in t. Must have the same shape as R unless the make_grid keyword is set. If the make_grid keyword is True, Z must have exactly one dimension.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of R, Z. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as R and Z (or their meshgrid if make_grid is True).
Keyword Arguments:
 
  • each_t (Boolean) – When True, the elements in R, Z are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of R and Z or be a scalar. Default is True (evaluate ALL R, Z at EACH element in t).
  • make_grid (Boolean) – Set to True to pass R and Z through scipy.meshgrid() before evaluating. If this is set to True, R and Z must each only have a single dimension, but can have different lengths. Default is False (do not form meshgrid).
  • length_unit (String or 1) –

    Length unit that R, Z are given in. If a string is given, it must be a valid unit specifier:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ meters

    If length_unit is 1 or None, meters are assumed. The default value is 1 (use meters).

  • return_t (Boolean) – Set to True to return a tuple of (BR, time_idxs), where time_idxs is the array of time indices actually used in evaluating BR with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return BR).
Returns:

BR or (BR, time_idxs)

  • BR (Array or scalar float) - The major radial component of the magnetic field. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned. If R and Z both have the same shape then BR has this shape as well, unless the make_grid keyword was True, in which case BR has shape (len(Z), len(R)).
  • time_idxs (Array with same shape as BR) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single BR value at R=0.6m, Z=0.0m, t=0.26s:

BR_val = Eq_instance.rz2BR(0.6, 0, 0.26)

Find BR values at (R, Z) points (0.6m, 0m) and (0.8m, 0m) at the single time t=0.26s. Note that the Z vector must be fully specified, even if the values are all the same:

BR_arr = Eq_instance.rz2BR([0.6, 0.8], [0, 0], 0.26)

Find BR values at (R, Z) points (0.6m, 0m) at times t=[0.2s, 0.3s]:

BR_arr = Eq_instance.rz2BR(0.6, 0, [0.2, 0.3])

Find BR values at (R, Z, t) points (0.6m, 0m, 0.2s) and (0.5m, 0.2m, 0.3s):

BR_arr = Eq_instance.rz2BR([0.6, 0.5], [0, 0.2], [0.2, 0.3], each_t=False)

Find BR values on grid defined by 1D vector of radial positions R and 1D vector of vertical positions Z at time t=0.2s:

BR_mat = Eq_instance.rz2BR(R, Z, 0.2, make_grid=True)
rz2BZ(R, Z, t, return_t=False, make_grid=False, each_t=True, length_unit=1)[source]

Calculates the vertical component of the magnetic field at the given (R, Z, t) coordinates.

Uses

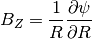
B_Z = \frac{1}{R}\frac{\partial \psi}{\partial R}

Parameters:
  • R (Array-like or scalar float) – Values of the radial coordinate to map to vertical field. If R and Z are both scalar values, they are used as the coordinate pair for all of the values in t. Must have the same shape as Z unless the make_grid keyword is set. If the make_grid keyword is True, R must have exactly one dimension.
  • Z (Array-like or scalar float) – Values of the vertical coordinate to map to vertical field. If R and Z are both scalar values, they are used as the coordinate pair for all of the values in t. Must have the same shape as R unless the make_grid keyword is set. If the make_grid keyword is True, Z must have exactly one dimension.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of R, Z. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as R and Z (or their meshgrid if make_grid is True).
Keyword Arguments:
 
  • each_t (Boolean) – When True, the elements in R, Z are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of R and Z or be a scalar. Default is True (evaluate ALL R, Z at EACH element in t).
  • make_grid (Boolean) – Set to True to pass R and Z through scipy.meshgrid() before evaluating. If this is set to True, R and Z must each only have a single dimension, but can have different lengths. Default is False (do not form meshgrid).
  • length_unit (String or 1) –

    Length unit that R, Z are given in. If a string is given, it must be a valid unit specifier:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ meters

    If length_unit is 1 or None, meters are assumed. The default value is 1 (use meters).

  • return_t (Boolean) – Set to True to return a tuple of (BZ, time_idxs), where time_idxs is the array of time indices actually used in evaluating BZ with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return BZ).
Returns:

BZ or (BZ, time_idxs)

  • BZ (Array or scalar float) - The vertical component of the magnetic field. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned. If R and Z both have the same shape then BZ has this shape as well, unless the make_grid keyword was True, in which case BZ has shape (len(Z), len(R)).
  • time_idxs (Array with same shape as BZ) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single BZ value at R=0.6m, Z=0.0m, t=0.26s:

BZ_val = Eq_instance.rz2BZ(0.6, 0, 0.26)

Find BZ values at (R, Z) points (0.6m, 0m) and (0.8m, 0m) at the single time t=0.26s. Note that the Z vector must be fully specified, even if the values are all the same:

BZ_arr = Eq_instance.rz2BZ([0.6, 0.8], [0, 0], 0.26)

Find BZ values at (R, Z) points (0.6m, 0m) at times t=[0.2s, 0.3s]:

BZ_arr = Eq_instance.rz2BZ(0.6, 0, [0.2, 0.3])

Find BZ values at (R, Z, t) points (0.6m, 0m, 0.2s) and (0.5m, 0.2m, 0.3s):

BZ_arr = Eq_instance.rz2BZ([0.6, 0.5], [0, 0.2], [0.2, 0.3], each_t=False)

Find BZ values on grid defined by 1D vector of radial positions R and 1D vector of vertical positions Z at time t=0.2s:

BZ_mat = Eq_instance.rz2BZ(R, Z, 0.2, make_grid=True)
rz2BT(R, Z, t, **kwargs)[source]

Calculates the toroidal component of the magnetic field at the given (R, Z, t).

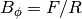Uses B_\phi = F / R.

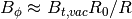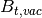By default, EFIT only computes this inside the LCFS. To approximate the field outside of the LCFS, B_\phi \approx B_{t, vac} R_0 / R is used, where B_{t, vac} is obtained with getBtVac() and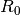 R_0 is the major radius of the magnetic axis obtained from getMagR().

The coordinate system used is right-handed, such that “forward” field on Alcator C-Mod (clockwise when seen from above) has negative BT.

Parameters:
  • R (Array-like or scalar float) – Values of the radial coordinate to map to BT. If R and Z are both scalar values, they are used as the coordinate pair for all of the values in t. Must have the same shape as Z unless the make_grid keyword is set. If the make_grid keyword is True, R must have exactly one dimension.
  • Z (Array-like or scalar float) – Values of the vertical coordinate to map to BT. If R and Z are both scalar values, they are used as the coordinate pair for all of the values in t. Must have the same shape as R unless the make_grid keyword is set. If the make_grid keyword is True, Z must have exactly one dimension.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of R, Z. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as R and Z (or their meshgrid if make_grid is True).
Keyword Arguments:
 
  • each_t (Boolean) – When True, the elements in R, Z are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of R and Z or be a scalar. Default is True (evaluate ALL R, Z at EACH element in t).
  • make_grid (Boolean) – Set to True to pass R and Z through scipy.meshgrid() before evaluating. If this is set to True, R and Z must each only have a single dimension, but can have different lengths. Default is False (do not form meshgrid).
  • length_unit (String or 1) –

    Length unit that R, Z are given in. If a string is given, it must be a valid unit specifier:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ meters

    If length_unit is 1 or None, meters are assumed. The default value is 1 (use meters).

  • return_t (Boolean) – Set to True to return a tuple of (BT, time_idxs), where time_idxs is the array of time indices actually used in evaluating BT with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return BT).
Returns:

BT or (BT, time_idxs)

  • BT (Array or scalar float) - The toroidal magnetic field. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned. If R and Z both have the same shape then BT has this shape as well, unless the make_grid keyword was True, in which case BT has shape (len(Z), len(R)).
  • time_idxs (Array with same shape as BT) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single BT value at R=0.6m, Z=0.0m, t=0.26s:

BT_val = Eq_instance.rz2BT(0.6, 0, 0.26)

Find BT values at (R, Z) points (0.6m, 0m) and (0.8m, 0m) at the single time t=0.26s. Note that the Z vector must be fully specified, even if the values are all the same:

BT_arr = Eq_instance.rz2BT([0.6, 0.8], [0, 0], 0.26)

Find BT values at (R, Z) points (0.6m, 0m) at times t=[0.2s, 0.3s]:

BT_arr = Eq_instance.rz2BT(0.6, 0, [0.2, 0.3])

Find BT values at (R, Z, t) points (0.6m, 0m, 0.2s) and (0.5m, 0.2m, 0.3s):

BT_arr = Eq_instance.rz2BT([0.6, 0.5], [0, 0.2], [0.2, 0.3], each_t=False)

Find BT values on grid defined by 1D vector of radial positions R and 1D vector of vertical positions Z at time t=0.2s:

BT_mat = Eq_instance.rz2BT(R, Z, 0.2, make_grid=True)
rz2B(R, Z, t, **kwargs)[source]

Calculates the magnitude of the magnetic field at the given (R, Z, t).

Parameters:
  • R (Array-like or scalar float) – Values of the radial coordinate to map to B. If R and Z are both scalar values, they are used as the coordinate pair for all of the values in t. Must have the same shape as Z unless the make_grid keyword is set. If the make_grid keyword is True, R must have exactly one dimension.
  • Z (Array-like or scalar float) – Values of the vertical coordinate to map to B. If R and Z are both scalar values, they are used as the coordinate pair for all of the values in t. Must have the same shape as R unless the make_grid keyword is set. If the make_grid keyword is True, Z must have exactly one dimension.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of R, Z. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as R and Z (or their meshgrid if make_grid is True).
Keyword Arguments:
 
  • each_t (Boolean) – When True, the elements in R, Z are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of R and Z or be a scalar. Default is True (evaluate ALL R, Z at EACH element in t).
  • make_grid (Boolean) – Set to True to pass R and Z through scipy.meshgrid() before evaluating. If this is set to True, R and Z must each only have a single dimension, but can have different lengths. Default is False (do not form meshgrid).
  • length_unit (String or 1) –

    Length unit that R, Z are given in. If a string is given, it must be a valid unit specifier:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ meters

    If length_unit is 1 or None, meters are assumed. The default value is 1 (use meters).

  • return_t (Boolean) – Set to True to return a tuple of (B, time_idxs), where time_idxs is the array of time indices actually used in evaluating B with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return B).
Returns:

B or (B, time_idxs)

  • B (Array or scalar float) - The magnitude of the magnetic field. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned. If R and Z both have the same shape then B has this shape as well, unless the make_grid keyword was True, in which case B has shape (len(Z), len(R)).
  • time_idxs (Array with same shape as B) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single B value at R=0.6m, Z=0.0m, t=0.26s:

B_val = Eq_instance.rz2B(0.6, 0, 0.26)

Find B values at (R, Z) points (0.6m, 0m) and (0.8m, 0m) at the single time t=0.26s. Note that the Z vector must be fully specified, even if the values are all the same:

B_arr = Eq_instance.rz2B([0.6, 0.8], [0, 0], 0.26)

Find B values at (R, Z) points (0.6m, 0m) at times t=[0.2s, 0.3s]:

B_arr = Eq_instance.rz2B(0.6, 0, [0.2, 0.3])

Find B values at (R, Z, t) points (0.6m, 0m, 0.2s) and (0.5m, 0.2m, 0.3s):

B_arr = Eq_instance.rz2B([0.6, 0.5], [0, 0.2], [0.2, 0.3], each_t=False)

Find B values on grid defined by 1D vector of radial positions R and 1D vector of vertical positions Z at time t=0.2s:

B_mat = Eq_instance.rz2B(R, Z, 0.2, make_grid=True)
rz2jR(R, Z, t, **kwargs)[source]

Calculates the major radial component of the current density at the given (R, Z, t) coordinates.

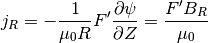
j_R = -\frac{1}{\mu_0 R}F'\frac{\partial \psi}{\partial Z} = \frac{F' B_R}{\mu_0}

Parameters:
  • R (Array-like or scalar float) – Values of the radial coordinate to map to radial current density. If R and Z are both scalar values, they are used as the coordinate pair for all of the values in t. Must have the same shape as Z unless the make_grid keyword is set. If the make_grid keyword is True, R must have exactly one dimension.
  • Z (Array-like or scalar float) – Values of the vertical coordinate to map to radial current density. If R and Z are both scalar values, they are used as the coordinate pair for all of the values in t. Must have the same shape as R unless the make_grid keyword is set. If the make_grid keyword is True, Z must have exactly one dimension.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of R, Z. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as R and Z (or their meshgrid if make_grid is True).
Keyword Arguments:
 
  • each_t (Boolean) – When True, the elements in R, Z are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of R and Z or be a scalar. Default is True (evaluate ALL R, Z at EACH element in t).
  • make_grid (Boolean) – Set to True to pass R and Z through scipy.meshgrid() before evaluating. If this is set to True, R and Z must each only have a single dimension, but can have different lengths. Default is False (do not form meshgrid).
  • length_unit (String or 1) –

    Length unit that R, Z are given in. If a string is given, it must be a valid unit specifier:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ meters

    If length_unit is 1 or None, meters are assumed. The default value is 1 (use meters).

  • return_t (Boolean) – Set to True to return a tuple of (jR, time_idxs), where time_idxs is the array of time indices actually used in evaluating jR with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return jR).
Returns:

jR or (jR, time_idxs)

  • jR (Array or scalar float) - The major radial component of the current density. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned. If R and Z both have the same shape then jR has this shape as well, unless the make_grid keyword was True, in which case jR has shape (len(Z), len(R)).
  • time_idxs (Array with same shape as jR) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single jR value at R=0.6m, Z=0.0m, t=0.26s:

jR_val = Eq_instance.rz2jR(0.6, 0, 0.26)

Find jR values at (R, Z) points (0.6m, 0m) and (0.8m, 0m) at the single time t=0.26s. Note that the Z vector must be fully specified, even if the values are all the same:

jR_arr = Eq_instance.rz2jR([0.6, 0.8], [0, 0], 0.26)

Find jR values at (R, Z) points (0.6m, 0m) at times t=[0.2s, 0.3s]:

jR_arr = Eq_instance.rz2jR(0.6, 0, [0.2, 0.3])

Find jR values at (R, Z, t) points (0.6m, 0m, 0.2s) and (0.5m, 0.2m, 0.3s):

jR_arr = Eq_instance.rz2jR([0.6, 0.5], [0, 0.2], [0.2, 0.3], each_t=False)

Find jR values on grid defined by 1D vector of radial positions R and 1D vector of vertical positions Z at time t=0.2s:

jR_mat = Eq_instance.rz2jR(R, Z, 0.2, make_grid=True)
rz2jZ(R, Z, t, **kwargs)[source]

Calculates the vertical component of the current density at the given (R, Z, t) coordinates.

Uses

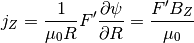
j_Z = \frac{1}{\mu_0 R}F'\frac{\partial \psi}{\partial R} = \frac{F' B_Z}{\mu_0}

Note that this function includes a factor of -1 to correct the FF’ from Alcator C-Mod’s EFIT implementation. You should check the sign of your data.

Parameters:
  • R (Array-like or scalar float) – Values of the radial coordinate to map to vertical current density. If R and Z are both scalar values, they are used as the coordinate pair for all of the values in t. Must have the same shape as Z unless the make_grid keyword is set. If the make_grid keyword is True, R must have exactly one dimension.
  • Z (Array-like or scalar float) – Values of the vertical coordinate to map to vertical current density. If R and Z are both scalar values, they are used as the coordinate pair for all of the values in t. Must have the same shape as R unless the make_grid keyword is set. If the make_grid keyword is True, Z must have exactly one dimension.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of R, Z. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as R and Z (or their meshgrid if make_grid is True).
Keyword Arguments:
 
  • each_t (Boolean) – When True, the elements in R, Z are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of R and Z or be a scalar. Default is True (evaluate ALL R, Z at EACH element in t).
  • make_grid (Boolean) – Set to True to pass R and Z through scipy.meshgrid() before evaluating. If this is set to True, R and Z must each only have a single dimension, but can have different lengths. Default is False (do not form meshgrid).
  • length_unit (String or 1) –

    Length unit that R, Z are given in. If a string is given, it must be a valid unit specifier:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ meters

    If length_unit is 1 or None, meters are assumed. The default value is 1 (use meters).

  • return_t (Boolean) – Set to True to return a tuple of (jZ, time_idxs), where time_idxs is the array of time indices actually used in evaluating jZ with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return jZ).
Returns:

jZ or (jZ, time_idxs)

  • jZ (Array or scalar float) - The vertical component of the current density. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned. If R and Z both have the same shape then jZ has this shape as well, unless the make_grid keyword was True, in which case jZ has shape (len(Z), len(R)).
  • time_idxs (Array with same shape as jZ) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single jZ value at R=0.6m, Z=0.0m, t=0.26s:

jZ_val = Eq_instance.rz2jZ(0.6, 0, 0.26)

Find jZ values at (R, Z) points (0.6m, 0m) and (0.8m, 0m) at the single time t=0.26s. Note that the Z vector must be fully specified, even if the values are all the same:

jZ_arr = Eq_instance.rz2jZ([0.6, 0.8], [0, 0], 0.26)

Find jZ values at (R, Z) points (0.6m, 0m) at times t=[0.2s, 0.3s]:

jZ_arr = Eq_instance.rz2jZ(0.6, 0, [0.2, 0.3])

Find jZ values at (R, Z, t) points (0.6m, 0m, 0.2s) and (0.5m, 0.2m, 0.3s):

jZ_arr = Eq_instance.rz2jZ([0.6, 0.5], [0, 0.2], [0.2, 0.3], each_t=False)

Find jZ values on grid defined by 1D vector of radial positions R and 1D vector of vertical positions Z at time t=0.2s:

jZ_mat = Eq_instance.rz2jZ(R, Z, 0.2, make_grid=True)
rz2jT(R, Z, t, **kwargs)[source]

Calculates the toroidal component of the current density at the given (R, Z, t) coordinates.

Uses

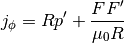
j_\phi = Rp' + \frac{FF'}{\mu_0 R}

The coordinate system used is right-handed, such that “forward” field on Alcator C-Mod (clockwise when seen from above) has negative jT.

Parameters:
  • R (Array-like or scalar float) – Values of the radial coordinate to map to toroidal current density. If R and Z are both scalar values, they are used as the coordinate pair for all of the values in t. Must have the same shape as Z unless the make_grid keyword is set. If the make_grid keyword is True, R must have exactly one dimension.
  • Z (Array-like or scalar float) – Values of the vertical coordinate to map to toroidal current density. If R and Z are both scalar values, they are used as the coordinate pair for all of the values in t. Must have the same shape as R unless the make_grid keyword is set. If the make_grid keyword is True, Z must have exactly one dimension.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of R, Z. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as R and Z (or their meshgrid if make_grid is True).
Keyword Arguments:
 
  • each_t (Boolean) – When True, the elements in R, Z are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of R and Z or be a scalar. Default is True (evaluate ALL R, Z at EACH element in t).
  • make_grid (Boolean) – Set to True to pass R and Z through scipy.meshgrid() before evaluating. If this is set to True, R and Z must each only have a single dimension, but can have different lengths. Default is False (do not form meshgrid).
  • length_unit (String or 1) –

    Length unit that R, Z are given in. If a string is given, it must be a valid unit specifier:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ meters

    If length_unit is 1 or None, meters are assumed. The default value is 1 (use meters).

  • return_t (Boolean) – Set to True to return a tuple of (jT, time_idxs), where time_idxs is the array of time indices actually used in evaluating jT with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return jT).
Returns:

jT or (jT, time_idxs)

  • jT (Array or scalar float) - The major radial component of the current density. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned. If R and Z both have the same shape then jT has this shape as well, unless the make_grid keyword was True, in which case jT has shape (len(Z), len(R)).
  • time_idxs (Array with same shape as jT) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single jT value at R=0.6m, Z=0.0m, t=0.26s:

jT_val = Eq_instance.rz2jT(0.6, 0, 0.26)

Find jT values at (R, Z) points (0.6m, 0m) and (0.8m, 0m) at the single time t=0.26s. Note that the Z vector must be fully specified, even if the values are all the same:

jT_arr = Eq_instance.rz2jT([0.6, 0.8], [0, 0], 0.26)

Find jT values at (R, Z) points (0.6m, 0m) at times t=[0.2s, 0.3s]:

jT_arr = Eq_instance.rz2jT(0.6, 0, [0.2, 0.3])

Find jT values at (R, Z, t) points (0.6m, 0m, 0.2s) and (0.5m, 0.2m, 0.3s):

jT_arr = Eq_instance.rz2jT([0.6, 0.5], [0, 0.2], [0.2, 0.3], each_t=False)

Find jT values on grid defined by 1D vector of radial positions R and 1D vector of vertical positions Z at time t=0.2s:

jT_mat = Eq_instance.rz2jT(R, Z, 0.2, make_grid=True)
rz2j(R, Z, t, **kwargs)[source]

Calculates the magnitude of the current density at the given (R, Z, t) coordinates.

Parameters:
  • R (Array-like or scalar float) – Values of the radial coordinate to map to current density magnitude. If R and Z are both scalar values, they are used as the coordinate pair for all of the values in t. Must have the same shape as Z unless the make_grid keyword is set. If the make_grid keyword is True, R must have exactly one dimension.
  • Z (Array-like or scalar float) – Values of the vertical coordinate to map to current density magnitude. If R and Z are both scalar values, they are used as the coordinate pair for all of the values in t. Must have the same shape as R unless the make_grid keyword is set. If the make_grid keyword is True, Z must have exactly one dimension.
  • t (Array-like or scalar float) – Times to perform the conversion at. If t is a single value, it is used for all of the elements of R, Z. If the each_t keyword is True, then t must be scalar or have exactly one dimension. If the each_t keyword is False, t must have the same shape as R and Z (or their meshgrid if make_grid is True).
Keyword Arguments:
 
  • each_t (Boolean) – When True, the elements in R, Z are evaluated at each value in t. If True, t must have only one dimension (or be a scalar). If False, t must match the shape of R and Z or be a scalar. Default is True (evaluate ALL R, Z at EACH element in t).
  • make_grid (Boolean) – Set to True to pass R and Z through scipy.meshgrid() before evaluating. If this is set to True, R and Z must each only have a single dimension, but can have different lengths. Default is False (do not form meshgrid).
  • length_unit (String or 1) –

    Length unit that R, Z are given in. If a string is given, it must be a valid unit specifier:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ meters

    If length_unit is 1 or None, meters are assumed. The default value is 1 (use meters).

  • return_t (Boolean) – Set to True to return a tuple of (j, time_idxs), where time_idxs is the array of time indices actually used in evaluating j with nearest-neighbor interpolation. (This is mostly present as an internal helper.) Default is False (only return j).
Returns:

j or (j, time_idxs)

  • j (Array or scalar float) - The magnitude of the current density. If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array is returned. If R and Z both have the same shape then j has this shape as well, unless the make_grid keyword was True, in which case j has shape (len(Z), len(R)).
  • time_idxs (Array with same shape as j) - The indices (in self.getTimeBase()) that were used for nearest-neighbor interpolation. Only returned if return_t is True.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single j value at R=0.6m, Z=0.0m, t=0.26s:

j_val = Eq_instance.rz2j(0.6, 0, 0.26)

Find j values at (R, Z) points (0.6m, 0m) and (0.8m, 0m) at the single time t=0.26s. Note that the Z vector must be fully specified, even if the values are all the same:

j_arr = Eq_instance.rz2j([0.6, 0.8], [0, 0], 0.26)

Find j values at (R, Z) points (0.6m, 0m) at times t=[0.2s, 0.3s]:

j_arr = Eq_instance.rz2j(0.6, 0, [0.2, 0.3])

Find j values at (R, Z, t) points (0.6m, 0m, 0.2s) and (0.5m, 0.2m, 0.3s):

j_arr = Eq_instance.rz2j([0.6, 0.5], [0, 0.2], [0.2, 0.3], each_t=False)

Find j values on grid defined by 1D vector of radial positions R and 1D vector of vertical positions Z at time t=0.2s:

j_mat = Eq_instance.rz2j(R, Z, 0.2, make_grid=True)
rz2FieldLineTrace(R0, Z0, t, phi0=0.0, field='B', num_rev=1.0, rev_method='toroidal', dphi=0.06283185307179587, integrator='dopri5')[source]

Trace a field line starting from a given (R, phi, Z) point.

Parameters:
  • R0 (float) – Major radial coordinate of starting point.
  • Z0 (float) – Vertical coordinate of starting point.
  • t (float) – Time to trace field line at.
Keyword Arguments:
 
  • phi0 (float) – Toroidal angle of starting point in radians. Default is 0.0.
  • field ({'B', 'j'}) – The field to use. Can be magnetic field (‘B’) or current density (‘j’). Default is ‘B’ (magnetic field).
  • num_rev (float) – The number of revolutions to trace the field line through. Whether this refers to toroidal or poloidal revolutions is determined by the rev_method keyword. Default is 1.0.
  • rev_method ('toroidal', 'poloidal') – Whether num_rev refers to the number of toroidal or poloidal revolutions the field line should make. Note that ‘poloidal’ only makes sense for close field lines. Default is ‘toroidal’.
  • dphi (float) – Toroidal step size, in radians. Default is 0.02*pi. The number of steps taken is then 2*pi times the number of toroidal rotations divided by dphi. This can be negative to trace a field line clockwise instead of counterclockwise.
  • integrator (str) – The integrator to use with scipy.integrate.ode. Default is ‘dopri5’ (explicit Dormand-Prince of order (4)5). Can also be an instance of scipy.integrate.ode for which the integrator and its options has been set.
Returns:

Containing the (R, Z, phi) coordinates.
Return type:

array, (nsteps + 1, 3)
rho2FieldLineTrace(rho, t, origin='psinorm', **kwargs)[source]

Trace a field line starting from a given normalized coordinate point.

The field line is started at the outboard midplane.

Parameters:
  • rho (float) – Flux surface label of starting point.
  • t (float) – Time to trace field line at.
Keyword Arguments:
 
  • origin ({'psinorm', 'phinorm', 'volnorm', 'r/a', 'Rmid', 'Fnorm'}) – The flux surface coordinates which rhovals is given in. Default is ‘psinorm’.
  • phi0 (float) – Toroidal angle of starting point in radians. Default is 0.0.
  • field ({'B', 'j'}) – The field to use. Can be magnetic field (‘B’) or current density (‘j’). Default is ‘B’ (magnetic field).
  • num_rev (float) – The number of revolutions to trace the field line through. Whether this refers to toroidal or poloidal revolutions is determined by the rev_method keyword. Default is 1.0.
  • rev_method ('toroidal', 'poloidal') – Whether num_rev refers to the number of toroidal or poloidal revolutions the field line should make. Note that ‘poloidal’ only makes sense for close field lines. Default is ‘toroidal’.
  • dphi (float) – Toroidal step size, in radians. Default is 0.02*pi. The number of steps taken is then 2*pi times the number of toroidal rotations divided by dphi. This can be negative to trace a field line clockwise instead of counterclockwise.
  • integrator (str) – The integrator to use with scipy.integrate.ode. Default is ‘dopri5’ (explicit Dormand-Prince of order (4)5). Can also be an instance of scipy.integrate.ode for which the integrator and its options has been set.
Returns:

Containing the (R, Z, phi) coordinates.
Return type:

array, (nsteps + 1, 3)
plotField(t, rhovals=6, rhomin=0.05, rhomax=0.95, color='b', cmap='plasma', alpha=0.5, arrows=True, linewidth=1.0, arrowlinewidth=3.0, a=None, **kwargs)[source]

Plot the field lines starting from a number of points.

The field lines are started at the outboard midplane.

If uniformly-spaced psinorm points are used, the spacing of the magnetic field lines will be directly proportional to the field strength, assuming a sufficient number of revolutions is traced.

Parameters:

t (float) – Time to trace field line at.
Keyword Arguments:
 
  • rhovals (int or array of int) – The number of uniformly-spaced rho points between rhomin and rhomax to use, or an explicit grid of rho points to use. Default is 6.
  • rhomin (float) – The minimum value of rho to use when using a uniformly-spaced grid. Default is 0.05.
  • rhomax (float) – The maximum value of rho to use when using a uniformly-spaced grid. Default is 0.95.
  • color (str) – The color to plot the field lines in. Default is ‘b’. If set to ‘sequential’, each field line will be a different color, in the sequence matplotlib assigns them. If set to ‘magnitude’, the coloring will be proportional to the magnitude of the field. Note that this is very time-consuming, as the limitations of matplotlib mean that each line segment must be plotted individually.
  • cmap (str) – The colormap to use when color is ‘magnitude’. Default is ‘plasma’, a perceptually uniform sequential colormap.
  • alpha (float) – The transparency to plot the field lines with. Default is 0.5.
  • arrows (bool) – If True, an arrowhead indicating the field direction will be drawn at the start of each field line. Default is True.
  • linewidth (float) – The line width to use when plotting the field lines. Default is 1.0.
  • arrowlinewidth (float) – The line width to use when plotting the arrows. Default is 3.0
  • a (matplotlib.axes._subplots.Axes3DSubplot) – The axes to plot the field lines on. Default is to make a new figure. Note that a colorbar will be drawn when color is magnitude, but only if a is not provided.
  • origin ({'psinorm', 'phinorm', 'volnorm', 'r/a', 'Rmid', 'Fnorm'}) – The flux surface coordinates which rhovals is given in. Default is ‘psinorm’.
  • phi0 (float) – Toroidal angle of starting point in radians. Default is 0.0.
  • field ({'B', 'j'}) – The field to use. Can be magnetic field (‘B’) or current density (‘j’). Default is ‘B’ (magnetic field).
  • num_rev (float) – The number of revolutions to trace the field line through. Whether this refers to toroidal or poloidal revolutions is determined by the rev_method keyword. Default is 1.0.
  • rev_method ('toroidal', 'poloidal') – Whether num_rev refers to the number of toroidal or poloidal revolutions the field line should make. Note that ‘poloidal’ only makes sense for close field lines. Default is ‘toroidal’.
  • dphi (float) – Toroidal step size, in radians. Default is 0.02*pi. The number of steps taken is then 2*pi times the number of toroidal rotations divided by dphi. This can be negative to trace a field line clockwise instead of counterclockwise.
  • integrator (str) – The integrator to use with scipy.integrate.ode. Default is ‘dopri5’ (explicit Dormand-Prince of order (4)5). Can also be an instance of scipy.integrate.ode for which the integrator and its options has been set.
Returns:

The figure and axis which the field lines were plotted in.
Return type:

(figure, axis)
getMagRSpline(length_unit=1, kind='nearest')[source]

Gets the univariate spline to interpolate R_mag as a function of time.

Only used if the instance was created with keyword tspline=True.

Keyword Arguments:
 
  • length_unit (String or 1) –

    Length unit that R_mag is returned in. If a string is given, it must be a valid unit specifier:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ meters

    If length_unit is 1 or None, meters are assumed. The default value is 1 (R_out returned in meters).

  • kind (String or non-negative int) – Specifies the type of interpolation to be performed in getting from t to R_mag. This is passed to scipy.interpolate.interp1d. Valid options are: ‘linear’, ‘nearest’, ‘zero’, ‘slinear’, ‘quadratic’, ‘cubic’ If this keyword is an integer, it specifies the order of spline to use. See the documentation for interp1d for more details. Default value is ‘cubic’ (3rd order spline interpolation) when trispline is True, ‘nearest’ otherwise.
Returns:

trispline.UnivariateInterpolator or

scipy.interpolate.interp1d to convert from t to MagR.
getMagZSpline(length_unit=1, kind='nearest')[source]

Gets the univariate spline to interpolate Z_mag as a function of time.

Generated for completeness of the core position calculation when using tspline = True

Keyword Arguments:
 
  • length_unit (String or 1) –

    Length unit that R_mag is returned in. If a string is given, it must be a valid unit specifier:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ meters

    If length_unit is 1 or None, meters are assumed. The default value is 1 (R_out returned in meters).

  • kind (String or non-negative int) – Specifies the type of interpolation to be performed in getting from t to Z_mag. This is passed to scipy.interpolate.interp1d. Valid options are: ‘linear’, ‘nearest’, ‘zero’, ‘slinear’, ‘quadratic’, ‘cubic’ If this keyword is an integer, it specifies the order of spline to use. See the documentation for interp1d for more details. Default value is ‘cubic’ (3rd order spline interpolation) when trispline is True, ‘nearest’ otherwise.
Returns:

trispline.UnivariateInterpolator or

scipy.interpolate.interp1d to convert from t to MagZ.
getRmidOutSpline(length_unit=1, kind='nearest')[source]

Gets the univariate spline to interpolate R_mid_out as a function of time.

Generated for completeness of the core position calculation when using tspline = True

Keyword Arguments:
 
  • length_unit (String or 1) –

    Length unit that R_mag is returned in. If a string is given, it must be a valid unit specifier:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ meters

    If length_unit is 1 or None, meters are assumed. The default value is 1 (R_out returned in meters).

  • kind (String or non-negative int) – Specifies the type of interpolation to be performed in getting from t to R_mid_out. This is passed to scipy.interpolate.interp1d. Valid options are: ‘linear’, ‘nearest’, ‘zero’, ‘slinear’, ‘quadratic’, ‘cubic’ If this keyword is an integer, it specifies the order of spline to use. See the documentation for interp1d for more details. Default value is ‘cubic’ (3rd order spline interpolation) when trispline is True, ‘nearest’ otherwise.
Returns:

trispline.UnivariateInterpolator or

scipy.interpolate.interp1d to convert from t to R_mid.
getAOutSpline(length_unit=1, kind='nearest')[source]

Gets the univariate spline to interpolate a_out as a function of time.

Keyword Arguments:
 
  • length_unit (String or 1) –

    Length unit that a_out is returned in. If a string is given, it must be a valid unit specifier:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ meters

    If length_unit is 1 or None, meters are assumed. The default value is 1 (a_out returned in meters).

  • kind (String or non-negative int) – Specifies the type of interpolation to be performed in getting from t to a_out. This is passed to scipy.interpolate.interp1d. Valid options are: ‘linear’, ‘nearest’, ‘zero’, ‘slinear’, ‘quadratic’, ‘cubic’ If this keyword is an integer, it specifies the order of spline to use. See the documentation for interp1d for more details. Default value is ‘cubic’ (3rd order spline interpolation) when trispline is True, ‘nearest’ otherwise.
Returns:

trispline.UnivariateInterpolator or

scipy.interpolate.interp1d to convert from t to a_out.
getBtVacSpline(kind='nearest')[source]

Gets the univariate spline to interpolate BtVac as a function of time.

Only used if the instance was created with keyword tspline=True.

Keyword Arguments:
 kind (String or non-negative int) – Specifies the type of interpolation to be performed in getting from t to BtVac. This is passed to scipy.interpolate.interp1d. Valid options are: ‘linear’, ‘nearest’, ‘zero’, ‘slinear’, ‘quadratic’, ‘cubic’ If this keyword is an integer, it specifies the order of spline to use. See the documentation for interp1d for more details. Default value is ‘cubic’ (3rd order spline interpolation) when trispline is True, ‘nearest’ otherwise.
Returns:
trispline.UnivariateInterpolator or
scipy.interpolate.interp1d to convert from t to BtVac.
getInfo()[source]

Abstract method. See child classes for implementation.

Returns namedtuple of instance parameters (shot, equilibrium type, size, timebase, etc.)

getTimeBase()[source]

Abstract method. See child classes for implementation.

Returns timebase array [t]

getFluxGrid()[source]

Abstract method. See child classes for implementation.

returns 3D grid of psi(r,z,t)
The array returned should have the following dimensions:
First dimension: time Second dimension: Z Third dimension: R
getRGrid()[source]

Abstract method. See child classes for implementation.

Returns vector of R-values for psiRZ grid [r]

getZGrid()[source]

Abstract method. See child classes for implementation.

Returns vector of Z-values for psiRZ grid [z]

getFluxAxis()[source]

Abstract method. See child classes for implementation.

Returns psi at magnetic axis [t]

getFluxLCFS()[source]

Abstract method. See child classes for implementation.

Returns psi a separatrix [t]

getRLCFS()[source]

Abstract method. See child classes for implementation.

Returns R-positions (n points) mapping LCFS [t,n]

getZLCFS()[source]

Abstract method. See child classes for implementation.

Returns Z-positions (n points) mapping LCFS [t,n]

remapLCFS()[source]

Abstract method. See child classes for implementation.

Overwrites stored R,Z positions of LCFS with explicitly calculated psinorm=1 surface. This surface is then masked using core.inPolygon() to only draw within vacuum vessel, the end result replacing RLCFS, ZLCFS with an R,Z array showing the divertor legs of the flux surface in addition to the core-enclosing closed flux surface.

getFluxVol()[source]

Abstract method. See child classes for implementation.

Returns volume contained within flux surface as function of psi [psi,t]. Psi assumed to be evenly-spaced grid on [0,1]

getVolLCFS()[source]

Abstract method. See child classes for implementation.

Returns plasma volume within LCFS [t]

getRmidPsi()[source]

Abstract method. See child classes for implementation.

Returns outboard-midplane major radius of flux surface [t,psi]

getF()[source]

Abstract method. See child classes for implementation.

Returns F=RB_{Phi}(Psi), often calculated for grad-shafranov solutions [psi,t]

getFluxPres()[source]

Abstract method. See child classes for implementation.

Returns calculated pressure profile [psi,t]. Psi assumed to be evenly-spaced grid on [0,1]

getFFPrime()[source]

Abstract method. See child classes for implementation.

Returns FF’ function used for grad-shafranov solutions [psi,t]

getPPrime()[source]

Abstract method. See child classes for implementation.

Returns plasma pressure gradient as a function of psi [psi,t]

getElongation()[source]

Abstract method. See child classes for implementation.

Returns LCFS elongation [t]

getUpperTriangularity()[source]

Abstract method. See child classes for implementation.

Returns LCFS upper triangularity [t]

getLowerTriangularity()[source]

Abstract method. See child classes for implementation.

Returns LCFS lower triangularity [t]

getShaping()[source]

Abstract method. See child classes for implementation.

Returns dimensionless shaping parameters for plasma. Namedtuple containing {LCFS elongation, LCFS upper/lower triangularity}

getMagR()[source]

Abstract method. See child classes for implementation.

Returns magnetic-axis major radius [t]

getMagZ()[source]

Abstract method. See child classes for implementation.

Returns magnetic-axis Z [t]

getAreaLCFS()[source]

Abstract method. See child classes for implementation.

Returns LCFS surface area [t]

getAOut()[source]

Abstract method. See child classes for implementation.

Returns outboard-midplane minor radius [t]

getRmidOut()[source]

Abstract method. See child classes for implementation.

Returns outboard-midplane major radius [t]

getGeometry()[source]

Abstract method. See child classes for implementation.

Returns dimensional geometry parameters Namedtuple containing {mag axis R,Z, LCFS area, volume, outboard-midplane major radius}

getQProfile()[source]

Abstract method. See child classes for implementation.

Returns safety factor q profile [psi,t] Psi assumed to be evenly-spaced grid on [0,1]

getQ0()[source]

Abstract method. See child classes for implementation.

Returns q on magnetic axis [t]

getQ95()[source]

Abstract method. See child classes for implementation.

Returns q on 95% flux surface [t]

getQLCFS()[source]

Abstract method. See child classes for implementation.

Returns q on LCFS [t]

getQ1Surf()[source]

Abstract method. See child classes for implementation.

Returns outboard-midplane minor radius of q=1 surface [t]

getQ2Surf()[source]

Abstract method. See child classes for implementation.

Returns outboard-midplane minor radius of q=2 surface [t]

getQ3Surf()[source]

Abstract method. See child classes for implementation.

Returns outboard-midplane minor radius of q=3 surface [t]

getQs()[source]

Abstract method. See child classes for implementation.

Returns specific q-profile values. Namedtuple containing {q0, q95, qLCFS, minor radius of q=1,2,3 surfaces}

getBtVac()[source]

Abstract method. See child classes for implementation.

Returns vacuum on-axis toroidal field [t]

getBtPla()[source]

Abstract method. See child classes for implementation.

Returns plasma on-axis toroidal field [t]

getBpAvg()[source]

Abstract method. See child classes for implementation.

Returns average poloidal field [t]

getFields()[source]

Abstract method. See child classes for implementation.

Returns magnetic-field values. Namedtuple containing {Btor on magnetic axis (plasma and vacuum), avg Bpol}

getIpCalc()[source]

Abstract method. See child classes for implementation.

Returns calculated plasma current [t]

getIpMeas()[source]

Abstract method. See child classes for implementation.

Returns measured plasma current [t]

getJp()[source]

Abstract method. See child classes for implementation.

Returns grid of calculated toroidal current density [t,z,r]

getBetaT()[source]

Abstract method. See child classes for implementation.

Returns calculated global toroidal beta [t]

getBetaP()[source]

Abstract method. See child classes for implementation.

Returns calculated global poloidal beta [t]

getLi()[source]

Abstract method. See child classes for implementation.

Returns calculated internal inductance of plasma [t]

getBetas()[source]

Abstract method. See child classes for implementation.

Returns calculated betas and inductance. Namedtuple of {betat,betap,Li}

getDiamagFlux()[source]

Abstract method. See child classes for implementation.

Returns diamagnetic flux [t]

getDiamagBetaT()[source]

Abstract method. See child classes for implementation.

Returns diamagnetic-loop toroidal beta [t]

getDiamagBetaP()[source]

Abstract method. See child classes for implementation.

Returns diamagnetic-loop poloidal beta [t]

getDiamagTauE()[source]

Abstract method. See child classes for implementation.

Returns diamagnetic-loop energy confinement time [t]

getDiamagWp()[source]

Abstract method. See child classes for implementation.

Returns diamagnetic-loop plasma stored energy [t]

getDiamag()[source]

Abstract method. See child classes for implementation.

Returns diamagnetic measurements of plasma parameters. Namedtuple of {diamag. flux, betat, betap from coils, tau_E from diamag., diamag. stored energy}

getWMHD()[source]

Abstract method. See child classes for implementation.

Returns calculated MHD stored energy [t]

getTauMHD()[source]

Abstract method. See child classes for implementation.

Returns calculated MHD energy confinement time [t]

getPinj()[source]

Abstract method. See child classes for implementation.

Returns calculated injected power [t]

getCurrentSign()[source]

Abstract method. See child classes for implementation.

Returns calculated current direction, where CCW = +

getWbdot()[source]

Abstract method. See child classes for implementation.

Returns calculated d/dt of magnetic stored energy [t]

getWpdot()[source]

Abstract method. See child classes for implementation.

Returns calculated d/dt of plasma stored energy [t]

getBCentr()[source]

Abstract method. See child classes for implementation.

Returns Vacuum Toroidal magnetic field at Rcent point [t]

getRCentr()[source]

Abstract method. See child classes for implementation.

Radial position for Vacuum Toroidal magnetic field calculation

getEnergy()[source]

Abstract method. See child classes for implementation.

Returns stored-energy parameters. Namedtuple of {stored energy, confinement time, injected power, d/dt of magnetic, plasma stored energy}

getParam(path)[source]

Abstract method. See child classes for implementation.

Backup function: takes parameter name for variable, returns variable directly. Acts as wrapper to direct data-access routines from within object.

getMachineCrossSection()[source]

Abstract method. See child classes for implementation.

Returns (R,Z) coordinates of vacuum wall cross-section for plotting/masking routines.

getMachineCrossSectionFull()[source]

Abstract method. See child classes for implementation.

Returns (R,Z) coordinates of machine wall cross-section for plotting routines. Returns a more detailed cross-section than getLimiter(), generally a vector map displaying non-critical cross-section information. If this is unavailable, this should point to self.getMachineCrossSection(), which pulls the limiter outline stored by default in data files e.g. g-eqdsk files.

gfile(time=None, nw=None, nh=None, shot=None, name=None, tunit='ms', title='EQTOOLS', nbbbs=100)[source]

Generates an EFIT gfile with gfile naming convention

Keyword Arguments:
 
  • time (scalar float) – Time of equilibrium to generate the gfile from. This will use the specified spline functionality to do so. Allows for it to be unspecified for single-time-frame equilibria.
  • nw (scalar integer) – Number of points in R. R is the major radius, and describes the ‘width’ of the gfile.
  • nh (scalar integer) – Number of points in Z. In cylindrical coordinates Z is the height, and nh describes the ‘height’ of the gfile.
  • shot (scalar integer) – The shot numer of the equilibrium. Used to help generate the gfile name if unspecified.
  • name (String) – Name of the gfile. If unspecified, will follow standard gfile naming convention (g+shot.time) under current python operating directory. This allows for it to be saved in other directories, etc.
  • tunit (String) – Specified unit for tin. It can only be ‘ms’ for milliseconds or ‘s’ for seconds.
  • title (String) – Title of the gfile on the first line. Name cannot exceed 10 digits. This is so that the style of the first line is preserved.
  • nbbbs (scalar integer) – Number of points to define the plasma seperatrix within the gfile. The points are defined equally spaced in angle about the plasma center. This will cause the x-point to be poorly defined.
Raises:

ValueError – If title is longer than 10 characters.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class (example shot number of 1001).

Generate a gfile at t=0.26s, output of g1001.26:

Eq_instance.gfile(.26)
plotFlux(fill=True, mask=True, lw=3.0, add_title=True)[source]

Plots flux contours directly from psi grid.

Returns the Figure instance created and the time slider widget (in case you need to modify the callback). f.axes contains the contour plot as the first element and the time slice slider as the second element.

Keyword Arguments:
 
  • fill (Boolean) – Set True to plot filled contours. Set False (default) to plot white-background color contours.
  • mask (Boolean) – Set True (default) to mask the contours according to the vacuum vessel outline.
  • lw (float) – Linewidth when plotting LCFS. Default is 3.0.
  • add_title (Boolean) – Set True (default) to add a figure title with the time indicated.

eqtools.eqdskreader module

This module contains the EqdskReader class, which creates Equilibrium class functionality for equilibria stored in eqdsk files from EFIT(a- and g-files).

Classes:
EqdskReader:
Class inheriting Equilibrium reading g- and a-files for equilibrium data.
class eqtools.eqdskreader.EqdskReader(shot=None, time=None, gfile=None, afile=None, length_unit='m', verbose=True)[source]

Bases: eqtools.core.Equilibrium

Equilibrium subclass working from eqdsk ASCII-file equilibria.

Inherits mapping and structural data from Equilibrium, populates equilibrium and profile data from g- and a-files for a selected shot and time window.

Create instance of EqdskReader.

Generates object and reads data from selected g-file (either manually set or autodetected based on user shot and time selection), storing as object attributes for usage in Equilibrium mapping methods.

Calling structure - user may call class with shot and time (ms) values, set by keywords (or positional placement allows calling without explicit keyword syntax). EqdskReader then attempts to construct filenames from the shot/time, of the form ‘g[shot].[time]’ and ‘a[shot].[time]’. Alternately, the user may skip this input and explicitly set paths to the g- and/or a-files, using the gfile and afile keyword arguments. If both types of calls are set, the explicit g-file and a-file paths override the auto-generated filenames from the shot and time.

Keyword Arguments:
 
  • shot (Integer) – Shot index.
  • time (Integer) – Time index (typically ms). Shot and Time used to autogenerate filenames.
  • gfile (String) – Manually selects ASCII file for equilibrium read.
  • afile (String) – Manually selects ASCII file for time-history read.
  • length_unit (String) – Flag setting length unit for equilibrium scales. Defaults to ‘m’ for lengths in meters.
  • verbose (Boolean) – When set to False, suppresses terminal outputs during CSV read. Defaults to True (prints terminal output).
Raises:
  • IOError – if both name/shot and explicit filenames are not set.
  • ValueError – if the g-file cannot be found, or if multiple valid g/a-files are found.

Examples

Instantiate EqdskReader for a given shot and time – will search current working directory for files of the form g[shot].[time] and a[shot].[time], suppressing terminal outputs:

edr = eqtools.EqdskReader(shot,time,verbose=False)

or:

edr = eqtools.EqdskReader(shot=shot,time=time,verbose=False)

Instantiate EqdskReader with explicit file paths gfile_path and afile_path:

edr = eqtools.EqdskReader(gfile=gfile_path,afile=afile_path)
getInfo()[source]

returns namedtuple of equilibrium information

Returns:namedtuple containing
shot shot index
time time point of g-file
nr size of R-axis of spatial grid
nz size of Z-axis of spatial grid
efittype EFIT calculation type (magnetic, kinetic, MSE)
readAFile(afile)[source]

Reads a-file (scalar time-history data) to pull additional equilibrium data not found in g-file, populates remaining data (initialized as None) in object.

Parameters:afile (String) – Path to ASCII a-file.
Raises:IOError – If afile is not found.
rz2psi(R, Z, *args, **kwargs)[source]

Calculates the non-normalized poloidal flux at the given (R, Z). Wrapper for Equilibrium.rz2psi masking out timebase dependence.

Parameters:
  • R (Array-like or scalar float) – Values of the radial coordinate to map to poloidal flux. If R and Z are both scalar, then a scalar psi is returned. R and Z must have the same shape unless the make_grid keyword is set. If make_grid is True, R must have shape (len_R,).
  • Z (Array-like or scalar float) – Values of the vertical coordinate to map to poloidal flux. If R and Z are both scalar, then a scalar psi is returned. R and Z must have the same shape unless the make_grid keyword is set. If make_grid is True, Z must have shape (len_Z,).

All keyword arguments are passed to the parent Equilibrium.rz2psi. Remaining arguments in *args are ignored.

Returns:non-normalized poloidal flux. If all input arguments are scalar, then psi is scalar. IF R and Z have the same shape, then psi has this shape as well. If make_grid is True, then psi has the shape (len_R, len_Z).
Return type:psi (Array-like or scalar float)

Examples

All assume that Eq_instance is a valid instance EqdskReader:

Find single psi value at R=0.6m, Z=0.0m:

psi_val = Eq_instance.rz2psi(0.6, 0)

Find psi values at (R, Z) points (0.6m, 0m) and (0.8m, 0m). Note that the Z vector must be fully specified, even if the values are all the same:

psi_arr = Eq_instance.rz2psi([0.6, 0.8], [0, 0])

Find psi values on grid defined by 1D vector of radial positions R and 1D vector of vertical positions Z:

psi_mat = Eq_instance.rz2psi(R, Z, make_grid=True)
rz2psinorm(R, Z, *args, **kwargs)[source]

Calculates the normalized poloidal flux at the given (R,Z). Wrapper for Equilibrium.rz2psinorm masking out timebase dependence.

Uses the definition:

\texttt{psi\_norm} = \frac{\psi - \psi(0)}{\psi(a) - \psi(0)}

Parameters:
  • R (Array-like or scalar float) – Values of the radial coordinate to map to normalized poloidal flux. Must have the same shape as Z unless the make_grid keyword is set. If the make_grid keyword is True, R must have shape (len_R,).
  • Z (Array-like or scalar float) – Values of the vertical coordinate to map to normalized poloidal flux. Must have the same shape as R unless the make_grid keyword is set. If the make_grid keyword is True, Z must have shape (len_Z,).

All keyword arguments are passed to the parent Equilibrium.rz2psinorm. Remaining arguments in *args are ignored.

Returns:non-normalized poloidal flux. If all input arguments are scalar, then psinorm is scalar. IF R and Z have the same shape, then psinorm has this shape as well. If make_grid is True, then psinorm has the shape (len_R, len_Z).
Return type:psinorm (Array-like or scalar float)

Examples

All assume that Eq_instance is a valid instance of EqdskReader:

Find single psinorm value at R=0.6m, Z=0.0m:

psi_val = Eq_instance.rz2psinorm(0.6, 0)

Find psinorm values at (R, Z) points (0.6m, 0m) and (0.8m, 0m). Note that the Z vector must be fully specified, even if the values are all the same:

psi_arr = Eq_instance.rz2psinorm([0.6, 0.8], [0, 0])

Find psinorm values on grid defined by 1D vector of radial positions R and 1D vector of vertical positions Z:

psi_mat = Eq_instance.rz2psinorm(R, Z, make_grid=True)
rz2phinorm(R, Z, *args, **kwargs)[source]

Calculates normalized toroidal flux at a given (R,Z), using

\texttt{phi} &= \int q(\psi)\,d\psi\\ \texttt{phi\_norm} &= \frac{\phi}{\phi(a)}

Wrapper for Equilibrium.rz2phinorm masking out timebase dependence.

Parameters:
  • R (Array-like or scalar float) – Values of the radial coordinate to map to normalized toroidal flux. Must have the same shape as Z unless the make_grid keyword is set. If the make_grid keyword is True, R must have shape (len_R,).
  • Z (Array-like or scalar float) – Values of the vertical coordinate to map to normalized toroidal flux. Must have the same shape as R unless the make_grid keyword is set. If the make_grid keyword is True, Z must have shape (len_Z,).

All keyword arguments are passed to the parent Equilibrium.rz2phinorm. Remaining arguments in *args are ignored.

Returns:non-normalized poloidal flux. If all input arguments are scalar, then phinorm is scalar. IF R and Z have the same shape, then phinorm has this shape as well. If make_grid is True, then phinorm has the shape (len_R, len_Z).
Return type:phinorm (Array-like or scalar float)

Examples

All assume that Eq_instance is a valid instance of EqdskReader.

Find single phinorm value at R=0.6m, Z=0.0m:

phi_val = Eq_instance.rz2phinorm(0.6, 0)

Find phinorm values at (R, Z) points (0.6m, 0m) and (0.8m, 0m). Note that the Z vector must be fully specified, even if the values are all the same:

phi_arr = Eq_instance.rz2phinorm([0.6, 0.8], [0, 0])

Find phinorm values on grid defined by 1D vector of radial positions R and 1D vector of vertical positions Z:

phi_mat = Eq_instance.rz2phinorm(R, Z, make_grid=True)
rz2volnorm(*args, **kwargs)[source]

Calculates the normalized flux surface volume.

Not implemented for EqdskReader, as necessary parameter is not read from a/g-files.

Raises:NotImplementedError – in all cases.
rz2rho(method, R, Z, t=False, sqrt=False, make_grid=False, k=3, length_unit=1)[source]

Convert the passed (R, Z) coordinates into one of several normalized coordinates. Wrapper for Equilibrium.rz2rho masking timebase dependence.

Parameters:
  • method (String) –

    Indicates which normalized coordinates to use. Valid options are:

    psinorm Normalized poloidal flux
    phinorm Normalized toroidal flux
    volnorm Normalized volume
  • R (Array-like or scalar float) – Values of the radial coordinate to map to normalized coordinate. Must have the same shape as Z unless the make_grid keyword is set. If the make_grid keyword is True, R must have shape (len_R,).
  • Z (Array-like or scalar float) – Values of the vertical coordinate to map to normalized coordinate. Must have the same shape as R unless the make_grid keyword is set. If the make_grid keyword is True, Z must have shape (len_Z,).
Keyword Arguments:
 
  • t (indeterminant) – Provides duck typing for inclusion of t values. Passed t values either as an Arg or Kwarg are neglected.
  • sqrt (Boolean) – Set to True to return the square root of normalized coordinate. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False (return normalized coordinate itself).
  • make_grid (Boolean) – Set to True to pass R and Z through meshgrid before evaluating. If this is set to True, R and Z must each only have a single dimension, but can have different lengths. Default is False (do not form meshgrid).
  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • length_unit (String or 1) –

    Length unit that R and Z are being given in. If a string is given, it must be a valid unit specifier:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ meters

    If length_unit is 1 or None, meters are assumed. The default value is 1 (R and Z given in meters).
Returns:

If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array instance is returned. If R and Z both have the same shape then rho has this shape as well. If the make_grid keyword was True then rho has shape (len(Z), len(R)).
Return type:

rho (Array-like or scalar float)
Raises:

ValueError – If method is not one of the supported values.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single psinorm value at R=0.6m, Z=0.0m:

psi_val = Eq_instance.rz2rho('psinorm', 0.6, 0)

Find psinorm values at (R, Z) points (0.6m, 0m) and (0.8m, 0m). Note that the Z vector must be fully specified, even if the values are all the same:

psi_arr = Eq_instance.rz2rho('psinorm', [0.6, 0.8], [0, 0])

Find psinorm values on grid defined by 1D vector of radial positions R and 1D vector of vertical positions Z:

psi_mat = Eq_instance.rz2rho('psinorm', R, Z, make_grid=True)
rz2rmid(R, Z, t=False, sqrt=False, make_grid=False, rho=False, k=3, length_unit=1)[source]

Maps the given points to the outboard midplane major radius, R_mid. Wrapper for Equilibrium.rz2rmid masking timebase dependence.

Based on the IDL version efit_rz2rmid.pro by Steve Wolfe.

Parameters:
  • R (Array-like or scalar float) – Values of the radial coordinate to map to midplane radius. Must have the same shape as Z unless the make_grid keyword is set. If the make_grid keyword is True, R must have shape (len_R,).
  • Z (Array-like or scalar float) – Values of the vertical coordinate to map to midplane radius. Must have the same shape as R unless the make_grid keyword is set. If the make_grid keyword is True, Z must have shape (len_Z,).
Keyword Arguments:
 
  • t (indeterminant) – Provides duck typing for inclusion of t values. Passed t values either as an Arg or Kwarg are neglected.
  • sqrt (Boolean) – Set to True to return the square root of midplane radius. Only the square root of positive values is taken. Negative values are replaced with zeros, consistent with Steve Wolfe’s IDL implementation efit_rz2rho.pro. Default is False (return R_mid itself).
  • make_grid (Boolean) – Set to True to pass R and Z through meshgrid before evaluating. If this is set to True, R and Z must each only have a single dimension, but can have different lengths. Default is False (do not form meshgrid).
  • rho (Boolean) – Set to True to return r/a (normalized minor radius) instead of R_mid. Default is False (return major radius, R_mid).
  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • length_unit (String or 1) –

    Length unit that R and Z are being given in AND that R_mid is returned in. If a string is given, it must be a valid unit specifier:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ meters

    If length_unit is 1 or None, meters are assumed. The default value is 1 (R and Z given in meters, R_mid returned in meters).
Returns:

If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array instance is returned. If R and Z both have the same shape then R_mid has this shape as well. If the make_grid keyword was True then R_mid has shape (len(Z), len(R)).
Return type:

R_mid (Array or scalar float)

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single R_mid value at R=0.6m, Z=0.0m:

R_mid_val = Eq_instance.rz2rmid(0.6, 0)

Find R_mid values at (R, Z) points (0.6m, 0m) and (0.8m, 0m). Note that the Z vector must be fully specified, even if the values are all the same:

R_mid_arr = Eq_instance.rz2rmid([0.6, 0.8], [0, 0])

Find R_mid values on grid defined by 1D vector of radial positions R and 1D vector of vertical positions Z:

R_mid_mat = Eq_instance.rz2rmid(R, Z, make_grid=True)
psinorm2rmid(psi_norm, t=False, rho=False, k=3, length_unit=1)[source]

Calculates the outboard R_mid location corresponding to the passed psi_norm (normalized poloidal flux) values.

Parameters:

psi_norm (Array-like or scalar float) – Values of the normalized poloidal flux to map to midplane radius.
Keyword Arguments:
 
  • t (indeterminant) – Provides duck typing for inclusion of t values. Passed t values either as an Arg or Kwarg are neglected.
  • rho (Boolean) – Set to True to return r/a (normalized minor radius) instead of R_mid. Default is False (return major radius, R_mid).
  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
  • length_unit (String or 1) –

    Length unit that R_mid is returned in. If a string is given, it must be a valid unit specifier:

    ’m’ meters
    ’cm’ centimeters
    ’mm’ millimeters
    ’in’ inches
    ’ft’ feet
    ’yd’ yards
    ’smoot’ smoots
    ’cubit’ cubits
    ’hand’ hands
    ’default’ meters

    If length_unit is 1 or None, meters are assumed. The default value is 1 (R_mid returned in meters).
Returns:

If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array instance is returned.
Return type:

R_mid (Array-like or scalar float)

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single R_mid value for psinorm=0.7:

R_mid_val = Eq_instance.psinorm2rmid(0.7)

Find R_mid values at psi_norm values of 0.5 and 0.7. Note that the Z vector must be fully specified, even if the values are all the same:

R_mid_arr = Eq_instance.psinorm2rmid([0.5, 0.7])
psinorm2volnorm(*args, **kwargs)[source]

Calculates the outboard R_mid location corresponding to psi_norm (normalized poloidal flux) values.

Not implemented for EqdskReader, as necessary parameter is not read from a/g-files.

Raises:NotImplementedError – in all cases.
psinorm2phinorm(psi_norm, t=False, k=3)[source]

Calculates the normalized toroidal flux corresponding to the passed psi_norm (normalized poloidal flux) values.

Parameters:

psi_norm (Array-like or scalar float) – Values of the normalized poloidal flux to map to normalized toroidal flux.
Keyword Arguments:
 
  • t (indeterminant) – Provides duck typing for inclusion of t values. Passed t values either as an Arg or Kwarg are neglected.
  • k (positive int) – The degree of polynomial spline interpolation to use in converting coordinates.
Returns:

If all of the input arguments are scalar, then a scalar is returned. Otherwise, a scipy Array instance is returned.
Return type:

phinorm (Array-like or scalar float)

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class.

Find single phinorm value for psinorm=0.7:

phinorm_val = Eq_instance.psinorm2phinorm(0.7)

Find phinorm values at psi_norm values of 0.5 and 0.7. Note that the Z vector must be fully specified, even if the values are all the same:

phinorm_arr = Eq_instance.psinorm2phinorm([0.5, 0.7])
getTimeBase()[source]

Returns EFIT time point.

Returns:1-element, 1D array of time in s. Returns array for consistency with Equilibrium implementations with time variation.
Return type:time (Array)
getCurrentSign()[source]

Returns the sign of the current, based on the check in Steve Wolfe’s IDL implementation efit_rz2psi.pro.

Returns:1 for positive current, -1 for reversed.
Return type:currentSign (Int)
getFluxGrid()[source]

Returns EFIT flux grid.

Returns:[1,r,z] Array of flux values. Includes 1-element time axis for consistency with Equilibrium implementations with time variation.
Return type:psiRZ (Array)
getRGrid(length_unit=1)[source]

Returns EFIT R-axis.

Returns:[r] array of R-axis values for RZ grid.
Return type:R (Array)
getZGrid(length_unit=1)[source]

Returns EFIT Z-axis.

Returns:[z] array of Z-axis values for RZ grid.
Return type:Z (Array)
getFluxAxis()[source]

Returns psi on magnetic axis.

Returns:[1] array of psi on magnetic axis. Returns array for consistency with Equilibrium implementations with time variation.
Return type:psi0 (Array)
getFluxLCFS()[source]

Returns psi at separatrix.

Returns:[1] array of psi at separatrix. Returns array for consistency with Equilibrium implementations with time variation.
Return type:psia (Array)
getRLCFS(length_unit=1)[source]

Returns array of R-values of LCFS.

Returns:[1,n] array of R values describing LCFS. Returns array for consistency with Equilibrium implementations with time variation.
Return type:RLCFS (Array)
getZLCFS(length_unit=1)[source]

Returns array of Z-values of LCFS.

Returns:[1,n] array of Z values describing LCFS. Returns array for consistency with Equilibrium implementations with time variation.
Return type:ZLCFS (Array)
remapLCFS(mask=False)[source]

Overwrites RLCFS, ZLCFS values pulled from EFIT with explicitly-calculated contour of psinorm=1 surface.

Keyword Arguments:
 mask (Boolean) – Set True to mask LCFS path to limiter outline (using inPolygon). Set False to draw full contour of psi = psiLCFS. Defaults to False.
getFluxVol()[source]

Returns volume contained within a flux surface as a function of psi.

Not implemented in EqdskReader, as required data is not stored in g/a-files.

Raises:NotImplementedError – in all cases.
getVolLCFS(length_unit=3)[source]

Returns volume with LCFS.

Returns:[1] array of plasma volume. Returns array for consistency with Equilibrium implementations with time variation.
Return type:Vol (Array)
Raises:ValueError – if a-file data is not read.
getRmidPsi()[source]

Returns outboard-midplane major radius of flux surfaces.

Data not read from a/g-files, not implemented for EqdskReader.

Raises:NotImplementedError – in all cases.
getF()[source]

returns F=RB_{Phi}(Psi), calculated for grad-shafranov solutions [psi,t]

Returns:[1,n] array of F(psi). Returns array for consistency with Equilibrium implementations with time variation.
Return type:F (Array)
getFluxPres()[source]

Returns pressure on flux surface p(psi).

Returns:[1,n] array of pressure. Returns array for consistency with Equilibrium implementations with time variation.
Return type:p (Array)
getFFPrime()[source]

returns FF’ function used for grad-shafranov solutions.

Returns:[1,n] array of FF’(psi). Returns array for consistency with Equilibrium implementations with time variation.
Return type:FF (Array)
getPPrime()[source]

returns plasma pressure gradient as a function of psi.

Returns:[1,n] array of pp’(psi). Returns array for consistency with Equilibrium implementations with time variation.
Return type:pp (Array)
getElongation()[source]

Returns elongation of LCFS.

Returns:[1] array of plasma elongation. Returns array for consistency with Equilibrium implementations with time variation.
Return type:kappa (Array)
Raises:ValueError – if a-file data is not read.
getUpperTriangularity()[source]

Returns upper triangularity of LCFS.

Returns:[1] array of plasma upper triangularity. Returns array for consistency with Equilibrium implementations with time variation.
Return type:delta (Array)
Raises:ValueError – if a-file data is not read.
getLowerTriangularity()[source]

Returns lower triangularity of LCFS.

Returns:[1] array of plasma lower triangularity. Returns array for consistency with Equilibrium implementations with time variation.
Return type:delta (Array)
Raises:ValueError – if a-file data is not read.
getShaping()[source]

Pulls LCFS elongation, upper/lower triangularity.

Returns:namedtuple containing [kappa,delta_u,delta_l].
Raises:ValueError – if a-file data is not read.
getMagR(length_unit=1)[source]

Returns major radius of magnetic axis.

Keyword Arguments:
 length_unit (String or 1) – length unit R is specified in. Defaults to 1 (default unit of rmagx, typically m).
Returns:[1] array of major radius of magnetic axis. Returns array for consistency with Equilibrium implementations with time variation.
Return type:magR (Array)
Raises:ValueError – if a-file data is not read.
getMagZ(length_unit=1)[source]

Returns Z of magnetic axis.

Keyword Arguments:
 length_unit (String or 1) – length unit Z is specified in. Defaults to 1 (default unit of zmagx, typically m).
Returns:[1] array of Z of magnetic axis. Returns array for consistency with Equilibrium implementations with time variation.
Return type:magZ (Array)
Raises:ValueError – if a-file data is not read.
getAreaLCFS(length_unit=2)[source]

Returns surface area of LCFS.

Keyword Arguments:
 length_unit (String or 2) – unit area is specified in. Defaults to 2 (default unit, typically m^2).
Returns:[1] array of surface area of LCFS. Returns array for consistency with Equilibrium implementations with time variation.
Return type:AreaLCFS (Array)
Raises:ValueError – if a-file data is not read.
getAOut(length_unit=1)[source]

Returns outboard-midplane minor radius of LCFS.

Keyword Arguments:
 length_unit (String or 1) – unit radius is specified in. Defaults to 1 (default unit, typically m).
Returns:[1] array of outboard-midplane minor radius at LCFS.
Return type:AOut (Array)
Raises:ValueError – if a-file data is not read.
getRmidOut(length_unit=1)[source]

Returns outboard-midplane major radius of LCFS.

Keyword Arguments:
 length_unit (String or 1) – unit radius is specified in. Defaults to 1 (default unit, typically m).
Returns:[1] array of outboard-midplane major radius at LCFS. Returns array for consistency with Equilibrium implementations with time variation.
Return type:Rmid (Array)
Raises:ValueError – if a-file data is not read.
getGeometry(length_unit=None)[source]

Pulls dimensional geometry parameters.

Keyword Arguments:
 length_unit (String) – length unit parameters are specified in. Defaults to None, using default units for individual getter methods for constituent parameters.
Returns:namedtuple containing [Rmag,Zmag,AreaLCFS,aOut,RmidOut]
Raises:ValueError – if a-file data is not read.
getQProfile()[source]

Returns safety factor q(psi).

Returns:[1,n] array of q(psi).
Return type:qpsi (Array)
getQ0()[source]

Returns safety factor q on-axis, q0.

Returns:[1] array of q(psi=0). Returns array for consistency with Equilibrium implementations with time variation.
Return type:q0 (Array)
Raises:ValueError – if a-file data is not read.
getQ95()[source]

Returns safety factor q at 95% flux surface.

Returns:[1] array of q(psi=0.95). Returns array for consistency with Equilibrium implementations with time variation.
Return type:q95 (Array)
Raises:ValueError – if a-file data is not read.
getQLCFS()[source]

Returns safety factor q at LCFS (interpolated).

Returns:[1] array of q* (interpolated). Returns array for consistency with Equilibrium implementations with time variation.
Return type:qLCFS (Array)
Raises:ValueError – if a-file data is not loaded.
getQ1Surf(length_unit=1)[source]

Returns outboard-midplane minor radius of q=1 surface.

Keyword Arguments:
 length_unit (String or 1) – unit of minor radius. Defaults to 1 (default unit, typically m)
Returns:[1] array of minor radius of q=1 surface. Returns array for consistency with Equilibrium implementations with time variation.
Return type:qr1 (Array)
Raises:ValueError – if a-file data is not read.
getQ2Surf(length_unit=1)[source]

Returns outboard-midplane minor radius of q=2 surface.

Keyword Arguments:
 length_unit (String or 1) – unit of minor radius. Defaults to 1 (default unit, typically m)
Returns:[1] array of minor radius of q=2 surface. Returns array for consistency with Equilibrium implementations with time variation.
Return type:qr2 (Array)
Raises:ValueError – if a-file data is not read.
getQ3Surf(length_unit=1)[source]

Returns outboard-midplane minor radius of q=3 surface.

Keyword Arguments:
 length_unit (String or 1) – unit of minor radius. Defaults to 1 (default unit, typically m)
Returns:[1] array of minor radius of q=3 surface. Returns array for consistency with Equilibrium implementations with time variation.
Return type:qr3 (Array)
Raises:ValueError – if a-file data is not read.
getQs(length_unit=1)[source]

Pulls q-profile data.

Keyword Arguments:
 length_unit (String or 1) – unit of minor radius. Defaults to 1 (default unit, typically m)
Returns:namedtuple containing [q0,q95,qLCFS,rq1,rq2,rq3]
Raises:ValueError – if a-file data is not read.
getBtVac()[source]

Returns vacuum toroidal field on-axis.

Returns:[1] array of vacuum toroidal field. Returns array for consistency with Equilibrium implementations with time variation.
Return type:BtVac (Array)
Raises:ValueError – if a-file data is not read.
getBtPla()[source]

Returns plasma toroidal field on-axis.

Returns:[1] array of toroidal field including plasma effects. Returns array for consistency with Equilibrium implementations with time variation.
Return type:BtPla (Array)
Raises:ValueError – if a-file data is not read.
getBpAvg()[source]

Returns average poloidal field.

Returns:[1] array of average poloidal field. Returns array for consistency with Equilibrium implementations with time variation.
Return type:BpAvg (Array)
Raises:ValueError – if a-file data is not read.
getFields()[source]

Pulls vacuum and plasma toroidal field, poloidal field data.

Returns:namedtuple containing [BtVac,BtPla,BpAvg]
Raises:ValueError – if a-file data is not read.
getIpCalc()[source]

Returns EFIT-calculated plasma current.

Returns:[1] array of EFIT-reconstructed plasma current. Returns array for consistency with Equilibrium implementations with time variation.
Return type:IpCalc (Array)
getIpMeas()[source]

Returns measured plasma current.

Returns:[1] array of measured plasma current. Returns array for consistency with Equilibrium implementations with time variation.
Return type:IpMeas (Array)
Raises:ValueError – if a-file data is not read.
getJp()[source]

Returns (r,z) grid of toroidal plasma current density.

Data not read from g-file, not implemented for EqdskReader.

Raises:NotImplementedError – In all cases.
getBetaT()[source]

Returns EFIT-calculated toroidal beta.

Returns:[1] array of average toroidal beta. Returns array for consistency with Equilibrium implementations with time variation.
Return type:BetaT (Array)
Raises:ValueError – if a-file data is not read.
getBetaP()[source]

Returns EFIT-calculated poloidal beta.

Returns:[1] array of average poloidal beta. Returns array for consistency with Equilibrium implementations with time variation.
Return type:BetaP (Array)
Raises:ValueError – if a-file data is not read
getLi()[source]

Returns internal inductance of plasma.

Returns:[1] array of internal inductance. Returns array for consistency with Equilibrium implementations with time variation.
Return type:Li (Array)
Raises:ValueError – if a-file data is not read.
getBetas()[source]

Pulls EFIT-calculated betas and internal inductance.

Returns:namedtuple containing [betat,betap,Li]
Raises:ValueError – if a-file data is not read.
getDiamagFlux()[source]

Returns diamagnetic flux.

Returns:[1] array of measured diamagnetic flux. Returns array for consistency with Equilibrium implementations with time variation.
Return type:Flux (Array)
Raises:ValueError – if a-file data is not read.
getDiamagBetaT()[source]

Returns diamagnetic-loop measured toroidal beta.

Returns:[1] array of measured diamagnetic toroidal beta. Returns array for consistency with Equilibrium implementations with time variation.
Return type:BetaT (Array)
Raises:ValueError – if a-file data is not read.
getDiamagBetaP()[source]

Returns diamagnetic-loop measured poloidal beta.

Returns:[1] array of measured diamagnetic poloidal beta. Returns array for consistency with
Return type:BetaP (Array)
Equilibrium
implementations with time variation.
Raises:ValueError – if a-file data is not read.
getDiamagTauE()[source]

Returns diamagnetic-loop energy confinement time.

Returns:[1] array of measured energy confinement time. Returns array for consistency with Equilibrium implementations with time variation.
Return type:TauE (Array)
Raises:ValueError – if a-file data is not read.
getDiamagWp()[source]

Returns diamagnetic-loop measured stored energy.

Returns:[1] array of diamagnetic stored energy. Returns array for consistency with Equilibrium implementations with time variation.
Return type:Wp (Array)
Raises:ValueError – if a-file data is not read.
getDiamag()[source]

Pulls diamagnetic flux, diamag. measured toroidal and poloidal beta, stored energy, and energy confinement time.

Returns:namedtuple containing [diaFlux,diaBetat,diaBetap,diaTauE,diaWp]
Raises:ValueError – if a-file data is not read
getWMHD()[source]

Returns EFIT-calculated stored energy.

Returns:[1] array of EFIT-reconstructed stored energy. Returns array for consistency with Equilibrium implementations with time variation.
Return type:WMHD (Array)
Raises:ValueError – if a-file data is not read.
getTauMHD()[source]

Returns EFIT-calculated energy confinement time.

Returns:[1] array of EFIT-reconstructed energy confinement time. Returns array for consistency with Equilibrium implementations with time variation.
Return type:tauMHD (Array)
Raises:ValueError – if a-file data is not read.
getPinj()[source]

Returns EFIT injected power.

Returns:[1] array of EFIT-reconstructed injected power. Returns array for consistency with Equilibrium implementations with time variation.
Return type:Pinj (Array)
Raises:ValueError – if a-file data is not read.
getWbdot()[source]

Returns EFIT d/dt of magnetic stored energy

Returns:[1] array of d(Wb)/dt. Returns array for consistency with Equilibrium implementations with time variation.
Return type:dWdt (Array)
Raises:ValueError – if a-file data is not read.
getWpdot()[source]

Returns EFIT d/dt of plasma stored energy.

Returns:[1] array of d(Wp)/dt. Returns array for consistency with Equilibrium implementations with time variation.
Return type:dWdt (Array)
Raises:ValueError – if a-file data is not read.
getBCentr()[source]

returns Vacuum toroidal magnetic field in Tesla at Rcentr

Returns:[nt] array of B_t at center [T]
Return type:B_cent (Array)
Raises:ValueError – if module cannot retrieve data from MDS tree.
getRCentr(length_unit=1)[source]

returns radius where Bcentr evaluated

Returns:Radial position where Bcent calculated [m]
Return type:R
Raises:ValueError – if module cannot retrieve data from MDS tree.
getEnergy()[source]

Pulls EFIT stored energy, energy confinement time, injected power, and d/dt of magnetic and plasma stored energy.

Returns:namedtuple containing [WMHD,tauMHD,Pinj,Wbdot,Wpdot]
Raises:ValueError – if a-file data is not read.
getParam(name)[source]

Backup function, applying a direct path input for tree-like data storage access for parameters not typically found in Equilbrium object. Directly calls attributes read from g/a-files in copy-safe manner.

Parameters:name (String) – Parameter name for value stored in EqdskReader instance.
Returns:value stored as attribute in EqdskReader.
Return type:param (Array-like or scalar float)
Raises:AttributeError – raised if no attribute is found.
getMachineCrossSection()[source]

Method to pull machine cross-section from data storage, convert to standard format for plotting routine.

Returns:(R_limiter, Z_limiter)
  • R_limiter (Array) - [n] array of x-values for machine cross-section.
  • Z_limiter (Array) - [n] array of y-values for machine cross-section.
getMachineCrossSectionFull()[source]

Returns vectorization of machine cross-section.

Absent additional data (not found in eqdsks) simply returns self.getMachineCrossSection().

gfile(time=None, nw=None, nh=None, shot=None, name=None, tunit='ms', title='EQTOOLS', nbbbs=100)[source]

Generates an EFIT gfile with gfile naming convention

Keyword Arguments:
 
  • time (scalar float) – Time of equilibrium to generate the gfile from. This will use the specified spline functionality to do so. Allows for it to be unspecified for single-time-frame equilibria.
  • nw (scalar integer) – Number of points in R. R is the major radius, and describes the ‘width’ of the gfile.
  • nh (scalar integer) – Number of points in Z. In cylindrical coordinates Z is the height, and nh describes the ‘height’ of the gfile.
  • shot (scalar integer) – The shot numer of the equilibrium. Used to help generate the gfile name if unspecified.
  • name (String) – Name of the gfile. If unspecified, will follow standard gfile naming convention (g+shot.time) under current python operating directory. This allows for it to be saved in other directories, etc.
  • tunit (String) – Specified unit for tin. It can only be ‘ms’ for milliseconds or ‘s’ for seconds.
  • title (String) – Title of the gfile on the first line. Name cannot exceed 10 digits. This is so that the style of the first line is preserved.
  • nbbbs (scalar integer) – Number of points to define the plasma seperatrix within the gfile. The points are defined equally spaced in angle about the plasma center. This will cause the x-point to be poorly defined.
Raises:

ValueError – If title is longer than 10 characters.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class (example shot number of 1001).

Generate a gfile (time at t=.26s) output of g1001.26:

Eq_instance.gfile()
plotFlux(fill=True, mask=True)[source]

streamlined plotting of flux contours directly from psi grid

Keyword Arguments:
 
  • fill (Boolean) – Default True. Set True to plot filled contours of flux delineated by black outlines. Set False to instead plot color-coded line contours on a blank background.
  • mask (Boolean) – Default True. Set True to draw a clipping mask based on the limiter outline for the flux contours. Set False to draw the full RZ grid.

eqtools.filewriter module

eqtools.filewriter.gfile(obj, tin, nw=None, nh=None, shot=None, name=None, tunit='ms', title='EQTOOLS', nbbbs=100)[source]

Generates an EFIT gfile with gfile naming convention

Parameters:
  • obj (eqtools Equilibrium Object) – Object which describes the tokamak This functionality is dependent on matplotlib, and is not not retained in core.py for this reason. It is a hidden function which takes an arbitrary equilibrium object and generates a gfile.
  • tin (scalar float) – Time of equilibrium to generate the gfile from. This will use the specified spline functionality to do so.
Keyword Arguments:
 
  • nw (scalar integer) – Number of points in R. R is the major radius, and describes the ‘width’ of the gfile.
  • nh (scalar integer) – Number of points in Z. In cylindrical coordinates Z is the height, and nh describes the ‘height’ of the gfile.
  • shot (scalar integer) – The shot numer of the equilibrium. Used to help generate the gfile name if unspecified.
  • name (String) – Name of the gfile. If unspecified, will follow standard gfile naming convention (g+shot.time) under current python operating directory. This allows for it to be saved in other directories, etc.
  • tunit (String) – Specified unit for tin. It can only be ‘ms’ for milliseconds or ‘s’ for seconds.
  • title (String) – Title of the gfile on the first line. Name cannot exceed 10 digits. This is so that the style of the first line is preserved.
  • nbbbs (scalar integer) – Number of points to define the plasma seperatrix within the gfile. The points are defined equally spaced in angle about the plasma center. This will cause the x-point to be poorly defined.
Raises:

ValueError – If title is longer than 10 characters.

Examples

All assume that Eq_instance is a valid instance of the appropriate extension of the Equilibrium abstract class (example shot number of 1001).

Generate a gfile at t=0.26s, output of g1001.26:

gfile(Eq_instance,.26)

eqtools.pfilereader module

This module contains the PFileReader class, a lightweight data handler for p-file (radial profile) datasets.

Classes:
PFileReader:
Data-storage class for p-file data. Reads data from ASCII p-file, storing as copy-safe object attributes.
class eqtools.pfilereader.PFileReader(pfile, verbose=True)[source]

Bases: object

Class to read ASCII p-file (profile data storage) into lightweight, user-friendly data structure.

P-files store data blocks containing the following: a header with parameter name, parameter units, x-axis units, and number of data points, followed by values of axis x, parameter y, and derivative dy/dx. Each parameter block is read into a namedtuple storing

‘name’ parameter name
‘npts’ array size
‘x’ abscissa array
‘y’ data array
‘dydx’ data gradient
‘xunits’ abscissa units
‘units’ data units

with each namedtuple stored as an attribute of the PFileReader instance. This gracefully handles variable formats of p-files (differing versions of p-files will have different parameters stored). Data blocks are accessed as attributes in a copy-safe manner.

Creates instance of PFileReader.

Parameters:pfile (String) – Path to ASCII p-file to be loaded.
Keyword Arguments:
 verbose (Boolean) – Option to print message on object creation listing available data parameters. Defaults to True.

Examples

Load p-file data located at file_path, while suppressing terminal output of stored parameters:

pfr = eqtools.PFileReader(file_path,verbose=False)

Recover electron density data (for example):

ne_data = pfr.ne

Recover abscissa and electron density data (for example):

ne = pfr.ne.y
abscis = pfr.ne.x

Available parameters in pfr may be listed via the overridden __str__ command.

eqtools.trispline module

This module provides interface to the tricubic spline interpolator. It also contains an enhanced bivariate spline which generates bounds errors.

class eqtools.trispline.Spline(x, y, z, f, boundary='natural', dx=0, dy=0, dz=0, bounds_error=True, fill_value=nan)[source]

Tricubic interpolating spline with forced edge derivative equal zero conditions. It assumes a cartesian grid. The ordering of f[z,y,x] is extremely important for the proper evaluation of the spline. It assumes that f is in C order.

Create a new Spline instance.

Parameters:
  • x (1-dimensional float array) – Values of the positions of the 1st Dimension of f. Must be monotonic without duplicates.
  • y (1-dimensional float array) – Values of the positions of the 2nd dimension of f. Must be monotonic without duplicates.
  • z (1-dimensional float array) – Values of the positions of the 3rd dimension of f. Must be monotonic without duplicates.
  • f (3-dimensional float array) – f[x,y,z]. NaN and Inf will hamper performance and affect interpolation in 4x4x4 space about its value.
Keyword Arguments:
 
  • regular (Boolean) – If the grid is known to be regular, forces matrix-based fast evaluation of interpolation.
  • fast (Boolean) – Outdated input to test the indexing performance of the c code vs internal python handling.
Raises:
  • ValueError – If any of the dimensions do not match specified f dim
  • ValueError – If x,y, or z are not monotonic

Examples

All assume that x, y, z, and f are valid instances of the appropriate numpy arrays which take independent variables x,y,z and create numpy array f. x1, y1, and z1 are numpy arrays which data f is to be interpolated.

Generate a Trispline instance map with data x, y, z and f:

map = Spline(x, y, z, f)

Evaluate Trispline instance map at x1, y1, z1:

output = map.ev(x1, y1, z1)
ev(xi, yi, zi, dx=0, dy=0, dz=0)[source]

evaluates tricubic spline at point (xi,yi,zi) which is f[xi,yi,zi].

Parameters:
  • xi (scalar float or 1-dimensional float) – Position in x dimension. This is the first dimension of 3d-valued grid.
  • yi (scalar float or 1-dimensional float) – Position in y dimension. This is the second dimension of 3d-valued grid.
  • zi (scalar float or 1-dimensional float) – Position in z dimension. This is the third dimension of 3d-valued grid.
Returns:

The interpolated value at (xi,yi,zi).
Return type:

val (array or scalar float)
Raises:

ValueError – If any of the dimensions exceed the evaluation boundary of the grid
class eqtools.trispline.RectBivariateSpline(x, y, z, bbox=[None, None, None, None], kx=3, ky=3, s=0, bounds_error=True, fill_value=nan)[source]

Bases: scipy.interpolate.fitpack2.RectBivariateSpline

the lack of a graceful bounds error causes the fortran to fail hard. This masks scipy.interpolate.RectBivariateSpline with a proper bound checker and value filler such that it will not fail in use for EqTools

Can be used for both smoothing and interpolating data.

Parameters:
  • x (1-dimensional float array) – 1-D array of coordinates in monotonically increasing order.
  • y (1-dimensional float array) – 1-D array of coordinates in monotonically increasing order.
  • z (2-dimensional float array) – 2-D array of data with shape (x.size,y.size).
Keyword Arguments:
 
  • bbox (1-dimensional float) – Sequence of length 4 specifying the boundary of the rectangular approximation domain. By default, bbox=[min(x,tx),max(x,tx), min(y,ty),max(y,ty)].
  • kx (integer) – Degrees of the bivariate spline. Default is 3.
  • ky (integer) – Degrees of the bivariate spline. Default is 3.
  • s (float) – Positive smoothing factor defined for estimation condition, sum((w[i]*(z[i]-s(x[i], y[i])))**2, axis=0) <= s Default is s=0, which is for interpolation.
ev(xi, yi)[source]
Evaluate the rectBiVariateSpline at (xi,yi). (x,y)values are
checked for being in the bounds of the interpolated data.
Parameters:
  • xi (float array) – input x dimensional values
  • yi (float array) – input x dimensional values
Returns:

evaluated spline at points (x[i], y[i]), i=0,…,len(x)-1
Return type:

val (float array)
class eqtools.trispline.BivariateInterpolator(x, y, z)[source]

Bases: object

This class provides a wrapper for scipy.interpolate.CloughTocher2DInterpolator.

This is necessary because scipy.interpolate.SmoothBivariateSpline cannot be made to interpolate, and gives inaccurate answers near the boundaries.

ev(xi, yi)[source]
class eqtools.trispline.UnivariateInterpolator(*args, **kwargs)[source]

Bases: scipy.interpolate.fitpack2.InterpolatedUnivariateSpline

Interpolated spline class which overcomes the shortcomings of interp1d (inaccurate near edges) and InterpolatedUnivariateSpline (can’t set NaN where it extrapolates).

Module contents

Provides classes for interacting with magnetic equilibrium data in a variety of formats.